1강. 이산수학의 개요
1. 연속에 대한 설명으로 바르지 않은 것은?
1) 연속이란 중단 또는 급격한 변화가 없는 상태이다.
2) 디지털 컴퓨터가 다루는 데이터는 연속적인 값이다.
3) 연속수학에는 미적분학, 위상수학, 해석학 등이 속한다.
4) 연속적인 성질을 가지는 수학 분야는 연속수학이라 한다.
정답: 2
해설: 디지털 컴퓨터가 다루는 데이터는 연속적인 값이 아니라 이산적인 값이다. 연속이란 중단 또는 급격한 변화가 없는 상태를 의미하며, 연속수학에는 미적분학, 위상수학, 해석학 등이 포함된다. 연속적인 성질을 가지는 수학 분야를 연속수학이라 한다. 선택지 2번은 연속적인 값이 아닌 이산적인 값을 다루기 때문에 바르지 않다.
2. 축구의 도구로 올바르지 않은 것은?
1) 골대
2) 축구장
3) 토털사커
4) 보호대
정답: 3
해설: 축구의 도구는 골대, 축구장, 보호대처럼 물리적인 장비를 포함한다. 토털사커는 축구의 전술이나 스타일을 의미하며 도구가 아니다. 골대는 골을 넣기 위해 필요하고, 축구장은 경기가 열리는 장소이며, 보호대는 선수의 안전을 위한 장비이다. 선택지 3번만이 도구가 아니라 축구의 전략이므로 올바르지 않다.
3. 다음 지문의 의사코드에서 주요하게 사용된 구조는?
for x ← 2 to 4
{
for y ← x to 3
{
print “*”
}
print “/”;
}
1) 순차구조
2) 선택구조
3) 반복구조
4) 조건구조
정답: 3
해설: 주어진 의사코드는 두 개의 for 루프를 사용하여 별을 출력하는 반복 구조를 보여준다. 첫 번째 for 루프는 x의 값을 2에서 4까지 증가시키고, 두 번째 for 루프는 y의 값을 x에서 3까지 증가시킨다. 이 중첩된 루프는 반복적인 작업을 수행하므로, 주요하게 사용된 구조는 반복구조이다. 선택구조와 조건구조는 특정 조건에 따라 흐름을 변경하지만, 여기서는 단순히 일정 범위 내에서 반복하는 구조만 존재한다.
4. 다음 중 추상화에 관하여 부적절한 서술은?
1) 추상화란 문제와 관련된 핵심내용을 제외한 것을 제거하는 것이다.
2) 논리회로는 변형시키거나 단순화 할 수 없다.
3) 수학적 추상모델은 문제 해결을 위해 다른 모델로 변형되기도 한다.
4) 컴퓨터 과학에서는 정보 모델링을 통해서 다양한 문제를 해결한다.
정답: 2
해설: 추상화란 문제와 관련된 핵심 내용을 제외한 것을 제거하는 것이다. 논리회로는 변형시키거나 단순화할 수 없다는 서술은 부적절하다. 논리회로 역시 추상화를 통해 단순화하거나 변형하여 더 효율적인 설계를 할 수 있다. 수학적 추상 모델은 문제 해결을 위해 다른 모델로 변형되기도 하고, 컴퓨터 과학에서는 정보 모델링을 통해 다양한 문제를 해결한다.
5. 알고리즘 표현 방법 중 틀린 것은?
1) 컴퓨터 프로그래밍 언어
2) 자연언어
3) 순서도
4) 의사코드
정답: 2
해설: 알고리즘 표현 방법으로는 컴퓨터 프로그래밍 언어, 순서도, 의사코드가 적절하다. 컴퓨터 프로그래밍 언어는 실제 코드로 알고리즘을 구현하는 방법이고, 순서도는 시각적으로 알고리즘의 흐름을 나타낸다. 의사코드는 자연어와 프로그래밍 언어의 중간 형태로 알고리즘을 설명한다. 그러나 자연언어는 모호성이 있어 명확하게 알고리즘을 표현하기 어렵다. 따라서 자연언어는 알고리즘 표현 방법으로 부적절하다.
2강 논리
1. 다음 중 명제인 것은?
1) 이번 시험 잘 보자
2) 해는 동쪽에서 떠서 서쪽으로 진다
3) 야 이것 참 아름답다
4) 지금 기분이 어때?
정답: 2
해설: 명제는 참과 거짓을 명확히 판단할 수 있는 문장이다. "해는 동쪽에서 떠서 서쪽으로 진다"는 참인 명제이다. 1번 "이번 시험 잘 보자"는 감탄문이고, 3번 "야 이것 참 아름답다"는 감정 표현이며, 4번 "지금 기분이 어때?"는 질문으로 명제가 아니다.
2. 다음 지문에서 명제 p, q에 대한 배타적 논리합 𝒑⨁𝒒 의 진리표는?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
3. 다음 지문에서 명제 p, q에 대한 합성명제 𝒓 ≡ ( 𝒑 ∨ 𝒒 ) ⨁ ( 𝒑 ∧ 𝒒 ) 의 진리표는?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 합성명제 \( r \equiv (p \lor q) \oplus (p \land q) \)의 진리표를 구하려면 각 경우에 대해 \( p \lor q \)와 \( p \land q \)를 계산하고, 두 결과의 XOR 연산을 수행한다. 선택지 3번은 \( p \)와 \( q \)의 조합에서 \( p \lor q \)와 \( p \land q \)의 XOR 결과가 \( r \)에 일치한다. 다른 선택지들은 일부 경우에서 일치하지 않는다.
4. 위 지문에서 조건명제 𝒑→𝒒 와 쌍조건명제 𝒑 ↔ 𝒒 의 진리표로 옳은 것은?

1 ① 번
2 ② 번
3 ③ 번
4 ④ 번
정답: 4
해설: 조건명제 \( p \to q \)는 \( p \)가 참이고 \( q \)가 거짓인 경우에만 거짓이며, 그 외에는 참이다. 쌍조건명제 \( p \leftrightarrow q \)는 \( p \)와 \( q \)가 같을 때 참이고, 다를 때 거짓이다. 선택지 4번은 조건명제와 쌍조건명제의 진리값이 각 경우에 맞게 정확히 표시되어 있다. 다른 선택지들은 이 명제들의 진리값이 올바르게 표현되지 않았다.
5. 다음 중 거짓인 명제는?
1) 한국의 수도가 서울이라면, 영국의 수도는 파리이다.
2)물의 분자식이 H₂ O₂ 이라면, 지구는 달을 공전한다.
3) 지구가 달을 공전한다. ↔ 물의 분자식이 H₂ O₂ 이다.
4) 1+2=5 ↔ 3+7=8
정답: 1
해설: 명제 1은 "한국의 수도가 서울이라면, 영국의 수도는 파리이다"로 구성되어 있는데, 이는 조건문으로 한국의 수도가 서울이라는 참인 명제에서 영국의 수도가 파리라는 거짓인 결론을 도출하여 거짓이다. 명제 2는 "물의 분자식이 $H_2O_2$이라면, 지구는 달을 공전한다"로 구성되어 있는데, 이는 전제가 거짓이므로 조건문 전체는 참이다. 명제 3은 "지구가 달을 공전한다 $\leftrightarrow$ 물의 분자식이 $H_2O_2$이다"로 구성되어 있는데, 이는 한쪽은 참, 한쪽은 거짓이므로 거짓이다. 명제 4는 "1+2=5 $\leftrightarrow$ 3+7=8"로 구성되어 있는데, 이는 두 명제 모두 거짓이므로 참이다.
명제 2는 전제가 거짓이기 때문에 조건문 전체는 항상 참이 된다. 명제 3은 "지구가 달을 공전한다"는 참이지만 "물의 분자식이 $H_2O_2$이다"는 거짓이므로 전체 명제는 거짓이 된다. 명제 4는 "1+2=5"와 "3+7=8"이 모두 거짓이기 때문에 전체 명제는 참이다. 따라서 정답은 1이다.
6. 조건 명제 “한국의 수도가 서울이라면, 영국의 수도는 파리이다”에 관련된 서술로서 옳은 것은?
1) 역은 “영국의 수도가 파리이면, 한국의 수도는 서울이다”가 된다.
2) 이는 “영국의 수도는 파리가 아니라면 한국의 수도가 서울이 아니다.”가 된다.
3) 대우는 “한국의 수도가 서울이 아니라면 영국의 수도는 파리가 아니다”가 된다.
4) 주어진 조건 명제의 진리값과 역의 진리값은 동일하다.
정답: 1
해설: 조건 명제 “한국의 수도가 서울이라면, 영국의 수도는 파리이다”의 역은 “영국의 수도가 파리이면, 한국의 수도는 서울이다”이다. 이는 주어진 명제에서 가정과 결론을 뒤바꾼 형태이다. 선택지 2번은 “영국의 수도가 파리가 아니라면 한국의 수도가 서울이 아니다”로, 이는 부정된 명제의 대우에 해당한다. 선택지 3번은 대우로, “한국의 수도가 서울이 아니라면 영국의 수도는 파리가 아니다”가 맞다. 선택지 4번은 일반적으로 조건 명제와 역의 진리값은 동일하지 않으므로 잘못된 서술이다. 선택지 1번이 주어진 조건 명제의 역을 올바르게 표현한 것이다.
7. 다음 중 항진명제가 아닌 것은?
1) 𝒑 ∨ ~ 𝒑
2) 𝒑 → 𝒒 ≡ ~ 𝒑 ∨ 𝒒
3) ~ ( 𝒑 ∨ 𝒒 ) ≡ (~ 𝒑 ) ∨ (~ 𝒒 )
4) (~ 𝒑 ∧ ~ 𝒒 ) ∨ ( ~ ( 𝒑 ∨ ~ 𝒒 )) ≡ ~ 𝒑
정답: 3
해설: 항진명제는 모든 경우에서 참이 되는 명제를 의미한다. 선택지 1번 \( \mathbb{p} \lor \sim \mathbb{p} \)는 항상 참이므로 항진명제이다. 선택지 2번 \( \mathbb{p} \rightarrow \mathbb{q} \equiv \sim \mathbb{p} \lor \mathbb{q} \)는 명제의 동치로 모든 경우에 참이다. 선택지 4번 \( \sim \mathbb{p} \land \sim \mathbb{q} \lor \sim ( \mathbb{p} \lor \sim \mathbb{q} ) \equiv \sim \mathbb{p} \)도 항상 참이므로 항진명제이다. 그러나 선택지 3번 \( \sim (\mathbb{p} \lor \mathbb{q}) \equiv (\sim \mathbb{p}) \lor (\sim \mathbb{q}) \)는 드모르간 법칙에 따라 \( \sim (\mathbb{p} \lor \mathbb{q}) \equiv (\sim \mathbb{p}) \land (\sim \mathbb{q}) \)로 표현되어 항진명제가 아니다. 따라서 선택지 3번이 항진명제가 아니다.
8. 명제함수 𝒑(𝒙, 𝒚) = 𝒙²+𝒚²=8 일 때, 𝒑(𝟏,𝟐)와 𝒑(𝟐,𝟐)의 진리값을 각각 구하면?
1) 𝒑(𝟏, 𝟐) = T , 𝒑(𝟐, 𝟐) = F
2) 𝒑(𝟏, 𝟐) = F , 𝒑(𝟐, 𝟐) = T
3) 𝒑(𝟏, 𝟐) = T , 𝒑(𝟐, 𝟐) = T
4) 𝒑(𝟏, 𝟐) = F , 𝒑(𝟐, 𝟐) = F
정답: 2
해설: 명제함수 \( p(x, y) = x^2 + y^2 = 8 \)에서 \( p(1, 2) \)와 \( p(2, 2) \)의 진리값을 구하면 다음과 같다. \( p(1, 2) \)는 \( 1^2 + 2^2 = 1 + 4 = 5 \)로 거짓(F)이다. \( p(2, 2) \)는 \( 2^2 + 2^2 = 4 + 4 = 8 \)로 참(T)이다. 따라서 \( p(1, 2) = F \)이고, \( p(2, 2) = T \)이므로 정답은 2번이다. 다른 선택지들은 각각 하나 또는 두 개의 진리값이 잘못되었다.
9. 명제함수 𝑷(𝒙)와 Q(𝒙)가 각각 𝑷(𝒙) = 𝒙² > 0, Q(𝒙) = 𝒙² + 𝟐𝒙 + 1 > 0 이고 𝒙의 정의역이 실수인 경우 다음 중 옳은 것은?
1) ∀𝒙 𝑷(𝒙)는 거짓이다.
2) ∀𝒙 Q(𝒙)는 참이다.
3) ∃𝒙 𝑷(𝒙)는 거짓이다.
4) ∃𝒙 𝑷(𝒙) ∧ ∀𝒙 Q(𝒙)는 참이다.
정답: 1
해설: 𝑷(𝒙) = 𝒙² > 0는 모든 실수 𝒙에 대해 성립하지 않으며, 𝒙 = 0일 때 거짓이므로 ∀𝒙 𝑷(𝒙)는 거짓이다. 𝑸(𝒙) = 𝒙² + 2𝒙 + 1 > 0는 𝒙의 정의역이 실수일 때 항상 성립하며, 이는 (𝒙+1)² > 0이기 때문에 𝒙 = -1을 제외하고 참이다. 따라서 ∀𝒙 𝑸(𝒙)는 거짓이므로 선택지 2는 틀리다. ∃𝒙 𝑷(𝒙)는 거짓이다는 ∃𝒙 𝑷(𝒙)가 적어도 하나의 𝒙에 대해 거짓임을 의미하지만, 𝑷(𝒙)는 𝒙 = 0이 아닌 모든 𝒙에 대해 참이므로 3번은 틀리다. ∃𝒙 𝑷(𝒙) ∧ ∀𝒙 𝑸(𝒙)는 적어도 하나의 𝒙에 대해 𝑷(𝒙)가 참이고 모든 𝒙에 대해 𝑸(𝒙)가 참이어야 하므로, 이 역시 틀리다. 따라서 정답은 1번이다.
10. 다음 지문의 명제가 항진명제인지 아닌지를 진리표를 이용하여 밝히시오.
① P ∨ T ≡ P
② P ∧ F ≡ F
③ ~ ~ P ≡ P
④ P ∧ P ≡ P
해설: 주어진 명제들의 항진명제 여부를 진리표를 통해 확인하다. 항진명제는 모든 경우에서 참인 명제를 의미한다.
1. **명제 ①: \( P \lor T \equiv P \)**
- 진리표:
\[
\begin{array}{|c|c|c|}
\hline
P & T & P \lor T \equiv P \\
\hline
T & T & T \\
F & T & F \\
\hline
\end{array}
\]
- 명제 \( P \lor T \)는 항상 참이므로 \( P \lor T \equiv T \)이다. 따라서 \( P \lor T \equiv P \)는 항진명제가 아니다.
2. **명제 ②: \( P \land F \equiv F \)**
- 진리표:
\[
\begin{array}{|c|c|c|}
\hline
P & F & P \land F \equiv F \\
\hline
T & F & F \\
F & F & F \\
\hline
\end{array}
\]
- 명제 \( P \land F \)는 항상 거짓이므로 \( P \land F \equiv F \)는 항상 참이다. 따라서 항진명제이다.
3. **명제 ③: \( \sim \sim P \equiv P \)**
- 진리표:
\[
\begin{array}{|c|c|c|}
\hline
P & \sim \sim P & \sim \sim P \equiv P \\
\hline
T & T & T \\
F & F & F \\
\hline
\end{array}
\]
- 이중 부정법에 의해 \( \sim \sim P \equiv P \)는 항상 참이다. 따라서 항진명제이다.
4. **명제 ④: \( P \land P \equiv P \)**
- 진리표:
\[
\begin{array}{|c|c|c|}
\hline
P & P \land P & P \land P \equiv P \\
\hline
T & T & T \\
F & F & F \\
\hline
\end{array}
\]
- 동일법칙에 의해 \( P \land P \equiv P \)는 항상 참이다. 따라서 항진명제이다.
결론적으로, 명제 ②, ③, ④는 항진명제이고, 명제 ①은 항진명제가 아니다.
11. 진리값이 참인 조건명제를 3개 작성하시오.
정답:
1. $A \rightarrow A$ (어떤 명제 $A$에 대해서도 $A$이면 $A$이다. 이는 항등법칙이다.)
2. $A \rightarrow (A \land B)$ (어떤 명제 $A$에 대해서 $A$이면 $A$이고 $B$이다. 이는 논리곱 도입법칙이다.)
3. $\neg B \rightarrow (B \rightarrow A)$ (명제 $B$가 거짓이면 $B$에서 $A$로의 조건명제는 참이다. 이는 논리적 의미로 참이다.)
해설: 첫 번째 조건명제 $A \rightarrow A$는 동일 법칙으로, 항상 참이다. 두 번째 조건명제 $A \rightarrow (A \land B)$는 $A$가 참이면 $A$와 $B$의 논리곱도 참이므로 참이다. 세 번째 조건명제 $\neg B \rightarrow (B \rightarrow A)$는 $B$가 거짓일 때 $B \rightarrow A$는 항상 참이기 때문에, $\neg B \rightarrow (B \rightarrow A)$도 항상 참이다. 이와 같이, 참인 조건명제는 논리적 법칙을 따르므로 항상 참이다.
12. 진리값이 거짓인 쌍조건명제를 3개 작성하시오.
정답:
거짓인 쌍조건명제는 두 명제의 진리값이 서로 다를 때 성립한다. 예를 들어, 명제 \( p \)와 \( q \)에 대해 \( p \leftrightarrow q \)가 거짓이 되는 경우를 찾으면 된다. 다음은 그러한 세 가지 예이다.
1. \( p \): "2는 소수이다." \( q \): "3은 짝수이다."
\( p \leftrightarrow q \)는 \( "2는 소수이다." \leftrightarrow "3은 짝수이다." \)로, \( p \)는 참이고 \( q \)는 거짓이므로 전체 명제는 거짓이다.
2. \( p \): "서울은 한국의 수도이다." \( q \): "파리는 독일의 수도이다."
\( p \leftrightarrow q \)는 \( "서울은 한국의 수도이다." \leftrightarrow "파리는 독일의 수도이다." \)로, \( p \)는 참이고 \( q \)는 거짓이므로 전체 명제는 거짓이다.
3. \( p \): "1은 자연수이다." \( q \): "0은 음수이다."
\( p \leftrightarrow q \)는 \( "1은 자연수이다." \leftrightarrow "0은 음수이다." \)로, \( p \)는 참이고 \( q \)는 거짓이므로 전체 명제는 거짓이다.
위 예시들은 \( p \leftrightarrow q \)에서 하나의 명제는 참이고 다른 하나는 거짓인 경우로, 이런 경우 쌍조건명제는 항상 거짓이다.
13. 명제함수 𝑷(𝒙) = 𝒙² - 2𝒙 - 5 > 0 의 진리값이 참이 되는 𝒙 의 조건을 구하시오.
정답: \( x < 1 - \sqrt{6} \) 또는 \( x > 1 + \sqrt{6} \)
해설: 명제함수 \( P(x) = x^2 - 2x - 5 > 0 \)의 진리값이 참이 되는 \( x \)의 조건을 구하기 위해 먼저 부등식 \( x^2 - 2x - 5 = 0 \)의 해를 구해야 한다. 이를 위해 이차방정식의 근의 공식을 사용하면 \( x = 1 \pm \sqrt{6} \)이다. 즉, 근은 \( x = 1 + \sqrt{6} \)와 \( x = 1 - \sqrt{6} \)이다. 이차함수의 그래프가 아래로 볼록한 포물선 형태임을 고려하면, 함수 \( P(x) \)는 이 두 근 사이에서 음수이고, 그 외의 구간에서 양수이다. 따라서 명제 \( P(x) \)가 참이 되려면 \( x \)는 \( 1 - \sqrt{6} \)보다 작거나 \( 1 + \sqrt{6} \)보다 커야 한다. 다른 선택지들은 함수의 부호 변화에 대한 분석이 틀리거나, 이차방정식의 근을 잘못 구한 결과이다.
14. 다음 지문에서 조건명제들의 역, 이, 대우를 각각 작성하시오.
(1) 해가 동쪽에서 뜬다면, 달은 서쪽에서 뜬다.
(2) 𝒙 > 0 이라면, 𝒙³ > 0 이다.
(3) ∀𝒙 𝑷(𝒙)가 거짓이라면, ∃𝒙 𝑷(𝒙)는 참이다.
정답:
(1) 해가 동쪽에서 뜬다면, 달은 서쪽에서 뜬다.
- 역: 달이 서쪽에서 뜬다면, 해는 동쪽에서 뜬다.
- 이: 달이 서쪽에서 뜨지 않는다면, 해는 동쪽에서 뜨지 않는다.
- 대우: 달이 서쪽에서 뜨지 않는다면, 해는 동쪽에서 뜨지 않는다.
(2) \(x > 0\)이라면, \(x^3 > 0\)이다.
- 역: \(x^3 > 0\)이라면, \(x > 0\)이다.
- 이: \(x^3 \leq 0\)이라면, \(x \leq 0\)이다.
- 대우: \(x^3 \leq 0\)이라면, \(x \leq 0\)이다.
(3) \(\forall x \ P(x)\)가 거짓이라면, \(\exists x \ P(x)\)는 참이다.
- 역: \(\exists x \ P(x)\)가 참이라면, \(\forall x \ P(x)\)가 거짓이다.
- 이: \(\exists x \ P(x)\)가 거짓이라면, \(\forall x \ P(x)\)가 참이다.
- 대우: \(\exists x \ P(x)\)가 거짓이라면, \(\forall x \ P(x)\)가 참이다.
돌발 1. 다음 명제 p, q와 이들의 논리곱 pq의 진리값을 순서대로 나타낸 것은?
𝑷 : 홀수와 홀수를 곱하면 짝수이다.
𝒒 : 홀수와 홀수를 더하면 짝수이다.
1) F, F, F
2) F, T, F
3) T, F, T
4) T, T, T
정답: 2
해설: 명제 \(P\)는 "홀수와 홀수를 곱하면 짝수이다"로, 이는 거짓이다(F) 왜냐하면 홀수와 홀수를 곱하면 홀수가 되기 때문이다. 명제 \(Q\)는 "홀수와 홀수를 더하면 짝수이다"로, 이는 참이다(T) 왜냐하면 홀수와 홀수를 더하면 항상 짝수가 되기 때문이다. 따라서 \(P\)와 \(Q\)의 논리곱 \(P \land Q\)는 \(F \land T\)로, 이는 거짓이다(F). 선택지 1은 \(Q\)의 진리값이 잘못되었고, 선택지 3과 4는 \(P\)의 진리값이 잘못되었다.
돌발 2. 다음 중 항진명제인 것은?
1) 𝑷 ∨ T = 𝑷
2) 𝑷 ∧ F = 𝑷
3) 𝑷 ∨ ~ 𝑷
4) 𝑷 ∧ ~ 𝑷
정답: 3
해설: 항진명제는 항상 참인 명제를 의미한다. 선택지 3) 𝑷 ∨ ¬𝑷는 𝑷가 참이든 거짓이든 항상 참이므로 항진명제이다. 선택지 1) 𝑷 ∨ T = T이므로 𝑷과 무관하게 항상 참이지만, 𝑷 = 𝑷가 되지 않기 때문에 항진명제가 아니다. 선택지 2) 𝑷 ∧ F = F로 항상 거짓이기 때문에 항진명제가 아니다. 선택지 4) 𝑷 ∧ ¬𝑷는 𝑷가 참이든 거짓이든 항상 거짓이므로 항진명제가 아니다. 따라서 항진명제는 선택지 3) 𝑷 ∨ ¬𝑷이다.
3강 증명
1. 다음 설명 중 바르지 않은 것은?
1) 공리란 별도의 증명 없이 참으로 이용되는 명제이다
2) 정의란 공리와 정의를 통해 참으로 확인된 명제이다.
3) 증명이란 하나의 명제가 참임을 확인하는 과정이다.
4) 정리에는 피타고라스의 정리, 이항정리, 나머지 정리 등이 있다.
정답: 2
해설: 정의는 수학적 개념을 명확히 하기 위해 설정한 설명이나 규칙이다. 1번 선택지에서 공리는 별도의 증명 없이 참으로 받아들여지는 명제이다. 3번 선택지에서 증명은 명제가 참임을 논리적으로 확인하는 과정이다. 4번 선택지에서 정리는 증명을 통해 참으로 입증된 명제로, 피타고라스의 정리, 이항정리, 나머지 정리가 이에 해당한다. 따라서 정의를 참으로 확인된 명제라고 설명한 2번 선택지가 바르지 않다.
2. 증명방법에 해당하지 않는 것은?
1) 직접증명법
2) 수학적 귀납법
3) 간접증명법
4) 귀납가정법
정답: 4
해설: 증명방법에는 직접증명법, 수학적 귀납법, 간접증명법이 포함된다. 직접증명법은 명제의 참을 직접 증명하는 방법이고, 수학적 귀납법은 첫 번째 단계에서 명제가 참임을 보인 후, 다음 단계가 참임을 유도하는 방법이다. 간접증명법은 명제의 부정을 가정하고 모순을 도출하여 원래 명제가 참임을 증명한다. 귀납가정법은 증명방법이 아니라 단순히 반복 관찰을 통해 결론을 도출하는 방법이다. 따라서 선택지 4번은 증명방법에 해당하지 않는다.
3. 모든 실수 𝒙, 𝒚 에 대해 𝒙 > 𝒚이면 𝒙² > 𝒚²에 대한 반례를 보이고자 한다. 올바른 반례는 어느 것인가?
1) 𝒙 = 0, 𝒚 = 1
2) 𝒙 = 0, 𝒚 = -1
3) 𝒙 = -1, 𝒚 = 1
4) 𝒙 = 1, 𝒚 = 0
정답: 2
해설: \( x > y \)이면 \( x^2 > y^2 \)가 항상 성립하지 않는다. 예를 들어 \( x = 0 \)이고 \( y = -1 \)인 경우, \( 0 > -1 \)이므로 \( x > y \)가 성립한다. 그러나 \( 0^2 = 0 \)이고 \( (-1)^2 = 1 \)이므로 \( x^2 < y^2 \)가 된다. 선택지 1) \( x = 0 \), \( y = 1 \)에서는 \( x > y \)가 성립하지 않으며, 선택지 3) \( x = -1 \), \( y = 1 \)에서는 \( -1 > 1 \)이 성립하지 않는다. 선택지 4) \( x = 1 \), \( y = 0 \)에서는 \( x > y \)이지만 \( x^2 > y^2 \)가 성립한다.
4. 수학적 귀납법의 과정 중 순서가 알맞은 것은?
1) 기본단계→귀납단계→귀납가정
2) 귀납단계→귀납가정→기본단계
3) 귀납가정→기본단계→귀납단계
4) 기본단계→귀납가정→귀납단계
정답: 4
해설: 수학적 귀납법의 과정은 세 단계로 이루어진다. 첫 번째는 기본 단계로, 귀납법의 시작점인 \(P(1)\)이 참임을 증명하는 단계이다. 두 번째는 귀납 가정으로, \(P(k)\)가 참이라고 가정한다. 세 번째는 귀납 단계로, \(P(k)\)가 참일 때 \(P(k+1)\)도 참임을 증명하여 \(P(n)\)이 모든 자연수 \(n\)에 대해 성립함을 보인다. 선택지 1번과 2번, 3번은 이 순서가 맞지 않아 부적절하다.
5. 다음 지문의 증명에서 사용된 증명 방법은 무엇인가 ?
“어떤 수 x 에 x 를 더한 것이 다시 x 이면, 그 수 x 는 0 이다.”를 증명한다.
가설은 x + x = x 이고, 결론은 x = 0이다.
증명을 위하여 x + x = x 이고 x ≠ 0라고 가정하자. 그러면 2x = x 이고 x ≠ 0 이다.
x ≠ = 0이므로 2x = x 의 양변을 나누면 2 = 1이라는 그릇된 결과를 얻는다.
따라서 (x + x = x) ⇒ (x = 0)이다.
1) 반증법
2) 수학적 귀납법
3) 모순 증명법
4) 직접 증명법
정답: 3
해설: 주어진 증명은 모순 증명법을 사용하고 있다. 모순 증명법은 어떤 명제가 참임을 보이기 위해 그 명제의 부정이 참이라고 가정한 후, 이로부터 모순이 발생함을 보여 원래 명제가 참임을 증명하는 방법이다. 여기서 "x ≠ 0"이라고 가정한 후, "2 = 1"이라는 모순을 유도하여 x = 0임을 증명한다. 반증법은 주어진 명제의 반대를 증명하여 원래 명제가 거짓임을 보이는 방법이고, 수학적 귀납법은 특정 조건이 모든 자연수에 대해 성립함을 보이는 방법이며, 직접 증명법은 명제를 직접적으로 증명하는 방법이다. 이 증명은 모순을 통해 원래 가정이 참임을 보이고 있으므로 모순 증명법이다.
6. 두 유리수의 합이 유리수임을 직접증명법으로 증명하시오.
해설: 두 유리수의 합이 유리수임을 증명하기 위해, 먼저 유리수의 정의를 사용한다. 유리수는 두 정수 \(a\)와 \(b\) (\(b \neq 0\))의 비로 표현되는 수 \(\frac{a}{b}\)이다. 두 유리수 \(\frac{a}{b}\)와 \(\frac{c}{d}\)를 더하면 \(\frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}\)가 된다. 여기서 \(ad + bc\)와 \(bd\)는 정수이므로, \(\frac{ad + bc}{bd}\)는 다시 유리수이다. 따라서 두 유리수의 합은 유리수임이 증명된다.
7. 소수는 완전수가 아님을 모순증명법으로 증명하시오.
해설: 소수는 약수가 1과 자기 자신뿐인 수이다. 만약 소수가 완전수라고 가정하면, 완전수의 정의에 따라 소수의 약수의 합은 자기 자신을 제외하고 자기 자신과 같아야 한다. 예를 들어, 소수 p가 완전수라면, 약수는 1과 p이며, 1 + p = p가 되어야 한다. 이는 1 = 0이 되어 모순이다. 따라서 소수는 완전수가 아니다.
다른 선지에 대해 설명하자면, 완전수는 자신을 제외한 모든 약수의 합이 자기 자신과 같은 수이다. 예를 들어, 6은 완전수로서 1, 2, 3의 약수를 가지며, 이들의 합은 6이다. 소수는 이러한 속성을 만족하지 않으므로, 소수는 완전수가 될 수 없다.
결론적으로, 소수는 완전수의 정의와 모순되므로 소수가 완전수일 수 없다는 것이 증명된다. 이로써 소수는 완전수가 아님을 모순 증명법으로 증명하였다.
8. 소수는 완전수가 아님을 모순증명법으로 증명하시오.
해설: 소수가 완전수가 아님을 모순증명법으로 증명하려면 소수가 완전수라고 가정하고 모순을 도출하면 된다. 완전수는 자신을 제외한 모든 양의 약수의 합이 자신과 같은 수이다. 예를 들어, 6은 1, 2, 3을 약수로 가지며 이들의 합은 6이다. 이제 소수 p가 완전수라고 가정하자. 소수 p의 약수는 1과 p 자신뿐이다. 완전수의 정의에 따라 1은 p 자신과 같아야 하므로 1 + 1 = p가 된다. 이는 p = 2이거나 p = 1이어야 한다는 것을 의미한다. 그러나 p가 2인 경우, 1 + 2 = 3이므로 완전수가 아니다. p가 1인 경우, 이는 소수가 아니라서 모순이 발생한다. 따라서 소수는 완전수가 아니다.
9. 𝒏 ≥ 5인 자연수에 대해 2ⁿ ≥ 𝒏²가 성립함을 수학적 귀납법으로 증명하시오.
해설: 수학적 귀납법으로 \(2^n \geq n^2\)를 증명하려면 먼저 \(n = 5\)에서 성립함을 보이고, \(n = k\)일 때 성립한다고 가정한 후 \(n = k+1\)에서도 성립함을 보여야 한다.
먼저 \(n = 5\)에서 \(2^5 = 32\)이고 \(5^2 = 25\)로 \(2^5 \geq 5^2\)이 성립한다.
다음으로 \(n = k\)에서 \(2^k \geq k^2\)가 성립한다고 가정한다. 이때 \(k \geq 5\)로 가정한다. \(2^{k+1} = 2 \cdot 2^k \geq 2 \cdot k^2\)이다. \(2 \cdot k^2 \geq (k+1)^2\)를 보이면 된다.
이를 전개하면 \(2k^2 \geq k^2 + 2k + 1\)로, \(k^2 \geq 2k + 1\)을 보이면 된다.
\(k \geq 5\)에서 \(k^2 \geq 2k + 1\)이 성립한다. 따라서 \(2^n \geq n^2\)는 \(n \geq 5\)에 대해 성립한다.
10. 모든 실수 ɑ에 대해 (ɑ+1)²≥ ɑ²가 성립하는지 반례 증명법으로 증명하시오.
해설: 이를 증명하기 위해 반례를 제시한다. \( \alpha = -1.5 \)일 때, \( (\alpha + 1)^2 = (-1.5 + 1)^2 = (-0.5)^2 = 0.25 \)이고 \( \alpha^2 = (-1.5)^2 = 2.25 \)이다. 따라서 \( (\alpha + 1)^2 = 0.25 < 2.25 = \alpha^2 \)가 되어 주어진 부등식이 성립하지 않음을 알 수 있다. 다른 반례로 \( \alpha = -1 \)을 선택하면 \( (\alpha + 1)^2 = 0 \)이고 \( \alpha^2 = 1 \)이므로 \( 0 < 1 \)로 부등식이 성립하지 않는다. 따라서 모든 실수 \( \alpha \)에 대해 \( (\alpha + 1)^2 \geq \alpha^2 \)가 성립하지 않는다.
4. 집합론
1. 다음 중 집합인 것은?
1) 1, 2, 3
2) {이산수학, 선형대수, 컴퓨터구조}
3) {서울, 대전, 서울, 대구, 광주}
4) { 1, 2, 3, 2, 3, 4 }
정답: 2
해설: 집합은 중복된 원소가 없고, 순서에 상관없는 원소들의 모임이다. 선택지 1은 숫자들이 콤마로 구분된 나열로 집합이 아니다. 선택지 2는 중복된 원소가 없고, 순서에 상관없이 과목들을 모아 놓은 집합이다. 선택지 3은 "서울"이 중복되므로 집합이 아니다. 선택지 4는 1, 2, 3이 중복되므로 집합이 아니다. 집합의 정의에 맞는 유일한 선택지는 2이다.
2. 집합 A = { 1, 2, 3 }과 동일한 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 집합 A = {1, 2, 3}과 동일한 집합은 원소가 1, 2, 3으로 이루어진 집합이다. ①번은 0과 4 사이의 실수로, 원소의 범위가 다르다. ②번은 0부터 4까지의 정수로 0과 4가 포함되어 있어 다르다. ③번은 0과 4 사이의 자연수로, 자연수 1, 2, 3을 포함하여 집합 A와 동일하다. ④번은 0부터 4까지의 자연수로 0과 4가 포함되어 있어 다르다. 따라서 집합 A와 동일한 집합은 ③번이다.
3. 다음과 같은 조건에서 올바른 서술은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 서로소 집합은 공통 원소가 없는 집합이다. \( A_1 \)과 \( A_2 \)를 비교하면, \( A_1 = \{a, b, c, d\} \)와 \( A_2 = \{e, f, g\} \)는 공통 원소가 없어 서로소이다. ②번에서 \( A_1 \)과 \( A_3 \)는 공통 원소 \(a, c\)가 있어 서로소가 아니다. ③번에서 \( A_2 \)와 \( A_4 \)는 공통 원소 \(f\)가 있어 서로소가 아니다. ④번에서 \(\{A_2, A_4\}\)는 분할이 되려면 A의 모든 원소를 포함해야 하지만 \(a, c, e, g\)가 빠져 있어 분할이 아니다. 따라서 올바른 서술은 ①번이다.
4. 집합 A = {a, b, c}의 분할로서 부적절한 것은?
1) { {a}, {b}, {c} }
2) { {a}, {b, c} }
3) { {a, b}, {b, c} }
4) { {a, b, c} }
정답: 3
해설: 집합의 분할은 각 부분집합이 서로 겹치지 않으며, 모든 부분집합의 합이 원래 집합이 되는 경우를 말한다. 선택지 3번의 { {a, b}, {b, c} }는 부분집합 {a, b}와 {b, c}에 원소 b가 중복되므로, 분할의 조건을 충족하지 않는다. 선택지 1번과 4번은 각각 모든 원소가 단일 원소 집합으로 나누어진 경우와 전체 집합이 하나의 부분집합으로 유지된 경우로, 적절한 분할이다. 선택지 2번도 {a}와 {b, c}로 겹치는 원소 없이 적절히 분할된 경우이다. 따라서 부적절한 분할은 선택지 3번이다.
5. 집합 A = {a, b, c}의 멱집합의 원소가 아닌 것은?
1) { }
2) { a }
3) { b, c }
4) { {a, b, c} }
정답: 4
해설: 집합 \( A = \{a, b, c\} \)의 멱집합은 모든 부분집합의 집합이다. 멱집합에는 공집합 \(\{\}\), 단일 원소 집합 \(\{a\}, \{b\}, \{c\}\), 이원소 집합 \(\{a, b\}, \{a, c\}, \{b, c\}\), 전체 집합 \(\{a, b, c\}\)가 포함된다. 따라서 1번 \(\{\}\), 2번 \(\{a\}\), 3번 \(\{b, c\}\)는 멱집합의 원소이다. 반면, 4번 \(\{\{a, b, c\}\}\)는 집합 \(A\)의 원소를 부분집합으로 갖는 것이 아니라, 집합 \(A\) 자체를 원소로 포함하여 멱집합의 원소가 될 수 없다.
6. U = {1, 2, 3, 4, 5}, A = {1, 2, 3}, B = {2, 3, 4}일 때 다음 지문중 틀린 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 지문 ④는 틀린 문장이다. 집합 \( A \cup B \)는 \( \{1, 2, 3, 4\} \)이며, \( A \cap B \)는 \( \{2, 3\} \)이다. \( A^C \)는 \( \{4, 5\} \)이고, \( B^C \)는 \( \{1, 5\} \)이다. 따라서 \( A^C \cup B^C \)는 \( \{1, 4, 5\} \)이다. 지문 ④에서 \( A^C \cup B^C = \{1, 4, 5\} \)와 다르기 때문에 틀리다. 다른 지문 ①, ②, ③은 모두 옳은 문장이다.
7. A = {1, 2, 3}일 때 다음 중 틀린 것은?
1) ① 번
2) ② 번
3) ③ 번
4) ④ 번

정답: 3
해설: 주어진 집합 \( A = \{1, 2, 3\} \)에 대해 각 항목을 검토한다. ① \( A \cup \emptyset = A \)는 공집합과의 합집합은 원래 집합이므로 옳다. ② \( A \cap \emptyset = \emptyset \)은 공집합과의 교집합은 공집합이므로 옳다. ③ \(|A \cup \emptyset| = |A| = 3\)로, 집합 \(A\)와 공집합의 합집합의 원소 개수는 3이어야 하므로 \(|A \cup \emptyset| = 0\)은 틀렸다. ④ \( P(A) \)는 집합 \( A \)의 멱집합으로, \( |P(A)| = 2^3 = 8 \)이므로 옳다. 따라서 정답은 3번이다.
8. 이산수학을 신청한 학생이 21명이고, 선형대수를 신청한 학생이 10명, 그리고 두 과목 모두 신청한 학생이 8명이였다. 이산수학 또는 선형대수를 신청한 학생은 모두 몇 명인가?
1) 13
2) 23
3) 29
4) 31
정답: 2
해설: 이산수학을 신청한 학생 수는 21명, 선형대수를 신청한 학생 수는 10명, 두 과목 모두를 신청한 학생 수는 8명이다. 따라서 이산수학 또는 선형대수를 신청한 학생 수는 두 집합의 합집합 크기를 의미하며, 이를 계산하기 위해 포함 배제 원리를 사용한다. 포함 배제 원리에 따르면, 두 과목 중 하나를 신청한 학생 수는 \(21 + 10 - 8 = 23\)명이다. 따라서 정답은 23명이다. 선택지 1번은 단순히 두 과목을 신청한 학생 수를 더하지 않아 부적절하고, 선택지 3번과 4번은 중복 학생 수를 두 번 포함하여 부적절하다.
9. U 가 전체집합이고 A, B, C 가 U 의 부분집합이라고 할 때, 다음 지문 중 올바른 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설:
10. U가 전체집합이고 A ⊆ B ⊆ U 일 때, 위 지문에서 틀린 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: \( A \cup (A \cap B) = A \)는 흡수 법칙으로 항상 참이다. \( (A^c)^c = A \)는 여집합의 여집합 법칙에 따라 참이다. \( A \cap A^c = U \)는 공집합이 되어야 하므로 거짓이다. \( A \cup (B \cap C) = (A \cup B) \cap C \)는 분배 법칙에 어긋나므로 거짓이다. 따라서 올바른 것은 ①번이다.
돌발 1. 전체 집합이 U 이고 집합 A 와 B 가 A ⊆ B 라 할 때, 다음 중 부적절한 것은?

1 ① 번
2 ② 번
3 ③ 번
4 ④ 번
정답: 1
해설: \( A \subseteq B \)일 때 \( A \cup B = B \)가 성립하므로 \( A \cup B = A \)는 부적절하다. \( A \cap B = A \)는 \( A \subseteq B \)일 때 항상 성립하며, \( A \cap B^c = \emptyset \)도 \( A \subseteq B \)에서 항상 참이다. \( A - B = \emptyset \) 역시 \( A \subseteq B \)일 때 성립한다. 따라서 부적절한 것은 ①번이다.
5. 행렬
1. 위 지문에서 값이 올바른 것은?

1) [ 1 1 0 0 ] , 1
2) [ 0 1 1 0 ] , 0
3) [ 0 1 1 0 ] , 1
4) [ 0 0 1 1 ] , 0
정답: 3
해설: 주어진 행렬 \( A \)는
\[
A =
\begin{bmatrix}
1 & 1 & 0 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 1 & 1
\end{bmatrix}
\]
이다. 2번째 행은 \([0 \, 1 \, 1 \, 0]\)이며, \(a_{33}\) 값은 \(A\)의 3번째 행 3번째 열의 원소로 1이다. 따라서 2번째 행이 \([0 \, 1 \, 1 \, 0]\)이고 \(a_{33} = 1\)인 3번이 올바르다. 다른 선택지들은 2번째 행 또는 \(a_{33}\)의 값을 잘못 제시하고 있다.
2. 행렬 A가 다음과 같은 때, 올바르지 않은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 주어진 행렬 \( A \)는
\[
A =
\begin{bmatrix}
1 & 0 & 0 & 1 \\
1 & 1 & 1 & 0 \\
1 & 0 & 1 & 1
\end{bmatrix}
\]
이다. 1번 선택지는 첫 번째 행이 \([1, 0, 0, 1]\)이어야 하는데, \([1, 0, 1, 1]\)로 잘못 제시되었다. 2번 선택지는 두 번째 행이 \([1, 1, 1, 0]\)으로 올바르게 제시되었다. 3번 선택지는 세 번째 열이 \([0, 1, 1]\)으로 올바르게 제시되었다. 4번 선택지는 네 번째 열이 \([1, 0, 1]\)으로 올바르게 제시되었다. 따라서 올바르지 않은 것은 1번이다.
3. 행렬 A와 B가 다음과 같을 때 2B-A를 구하면?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 행렬 \( A \)와 \( B \)가 주어졌을 때, 2B - A를 계산하면 된다. 먼저 행렬 B에 2를 곱하면 \( 2B = \begin{bmatrix} 4 & 2 & 2 & 2 \\ 2 & 2 & 4 & 6 \\ 6 & 2 & 4 & 0 \end{bmatrix} \)이다. 이제 2B에서 A를 빼면 \( 2B - A = \begin{bmatrix} 4-1 & 2-2 & 2-1 & 2-2 \\ 2-0 & 2-1 & 4-0 & 6-1 \\ 6-2 & 2-1 & 4-1 & 0-0 \end{bmatrix} = \begin{bmatrix} 3 & 0 & 1 & 0 \\ 2 & 1 & 4 & 5 \\ 4 & 1 & 3 & 0 \end{bmatrix} \)이다. 따라서 정답은 ④ 번의 행렬과 같다.
4. 행렬에 대한 다음 서술 중 부적절한 것은?
1) 모든 원소가 0인 행렬을 영행렬이라고 한다.
2) 정방행렬은 행의 수와 열의 수가 같은 행렬이다.
3) 행렬과 행렬의 곱연산은 교환법칙과 결합법칙이 성립한다.
4) 행렬의 모든 원소가 부울값으로만 구성된 행렬을 부울행렬이라고 한다.
정답: 3
해설: 행렬과 행렬의 곱연산에서 결합법칙은 성립하지만 교환법칙은 성립하지 않는다. 즉, 두 행렬 \(A\)와 \(B\)에 대해 \(A \cdot B \neq B \cdot A\)일 수 있다. 선택지 1번은 모든 원소가 0인 행렬을 영행렬이라고 정의하며, 이는 정확하다. 선택지 2번은 행과 열의 수가 같은 행렬을 정방행렬이라고 하며, 이 역시 정확하다. 선택지 4번은 행렬의 모든 원소가 부울값(0 또는 1)으로 구성된 행렬을 부울행렬이라고 하는데, 이것도 맞다. 따라서 선택지 3번의 행렬 곱 연산의 교환법칙 성립 여부가 틀린 설명이다.
5. 다음 행렬의 연산 법칙 중 올바르지 않은 것은?
1) A+B=B+A
2) (A+B)C= AC+BC
3) A+(-A)=O
4) A(BC)=(BC)A
정답: 4
해설: 정답 4번은 행렬 곱셈의 교환 법칙이 성립하지 않기 때문이다. 행렬 곱셈은 일반적으로 교환 법칙이 성립하지 않으며, $A(BC) \neq (BC)A$이다. 1번은 행렬 덧셈의 교환 법칙으로, $A + B = B + A$가 성립한다. 2번은 행렬 분배 법칙으로, $(A + B)C = AC + BC$가 성립한다. 3번은 행렬의 덧셈에 대한 역원 법칙으로, $A + (-A) = O$가 성립한다.
6. 행렬 A와 B가 다음 지문과 같을 때 행렬의 곱 A × B 를 구하면?
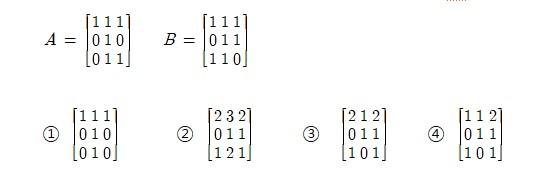
1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 2
해설: 행렬 $A$와 $B$를 곱하려면 $A \times B$를 계산한다. $A = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix}$, $B = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 0 \end{bmatrix}$를 곱하면, 결과는 $A \times B = \begin{bmatrix} 2 & 3 & 2 \\ 0 & 1 & 0 \\ 1 & 2 & 1 \end{bmatrix}$이다. 선택지 1번은 $A$와 동일한 행렬이고, 선택지 3번과 4번은 잘못된 결과이다. 따라서 올바른 결과는 선택지 2번이다.
7. 다음 일차연립방정식의 해를 가우스 소거법을 통해서 구하시오?
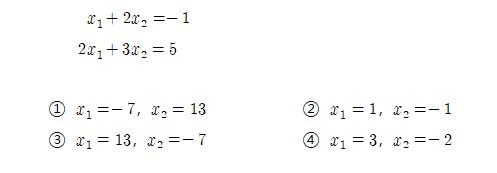
1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 가우스 소거법을 사용하여 주어진 연립방정식을 푼다. 먼저 주어진 방정식을 행렬 형태로 표현하면, $\begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -1 \\ 5 \end{bmatrix}$이다. 첫 번째 행을 2배하여 두 번째 행에서 빼면, 두 번째 행은 $\begin{bmatrix} 0 & -1 \end{bmatrix} \begin{bmatrix} x_2 \end{bmatrix} = \begin{bmatrix} -7 \end{bmatrix}$이 된다. 이를 풀면 $x_2 = -7$이고, 첫 번째 방정식에 대입하면 $x_1 = 13$이므로 해는 $x_1 = 13$, $x_2 = -7$이다. 따라서 정답은 3번이다.
8. 다음 지문의 행렬을 설명한 것으로 옳지 않은 것은?

1) 단위행렬
2) 대각행렬
3) 스칼라행렬
4) 대칭행렬
정답: 1
해설: 주어진 행렬은 $\begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{bmatrix}$로, 이 행렬은 모든 비대각선 원소가 0이고 대각선 원소가 같은 값을 가지므로 대각행렬, 스칼라행렬, 대칭행렬의 조건을 만족한다. 그러나 단위행렬은 대각선 원소가 모두 1이어야 하므로 이 행렬은 단위행렬이 아니다. 따라서 옳지 않은 설명은 1번이다.
9. 다음 행렬의 전치행렬로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 행렬 $A$의 전치행렬 $A^T$는 주대각선을 기준으로 행과 열을 바꾼 행렬이다. 주어진 행렬 $A$는 $\begin{bmatrix} 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \end{bmatrix}$이다. 이를 전치하면 $A^T = \begin{bmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \end{bmatrix}$이 된다. 선택지 1번, 2번, 4번은 잘못된 결과이다. 따라서 올바른 전치행렬은 선택지 3번이다.
10. 두 개의 부울행렬 A와 B가 다음과 같을 때 A와 B의 합(join)을 구하면?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 2
해설: 부울 행렬의 합(join)은 대응되는 원소 간의 논리합(OR)을 구하는 것이다. 주어진 행렬 $A$와 $B$는 각각 $\begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \end{bmatrix}$와 $\begin{bmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix}$이다. 각 원소별로 OR 연산을 수행하면 $\begin{bmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix}$가 된다. 따라서 정답은 2번이다. 다른 선택지들은 OR 연산 결과가 아니다.
돌발 1. 다음 행렬 A에 관한 서술로서 옳은 것은?

1) 단위행렬
2) 대각행렬
3) 대칭행렬
4) 삼각행렬
정답: 4
해설: 주어진 행렬 $A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 0 & 0 & 6 \end{pmatrix}$는 상삼각행렬이다. 상삼각행렬은 주대각선 아래의 모든 원소가 0인 행렬이다. 선택지 1번 단위행렬은 대각선 원소가 모두 1이어야 하고, 선택지 2번 대각행렬은 주대각선 이외의 모든 원소가 0이어야 하며, 선택지 3번 대칭행렬은 대각선을 기준으로 대칭이어야 한다. 따라서 옳은 서술은 4번이다.
돌발 2. 다음 두 부울행렬 A와 B의 부울곱을 구한 것으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 2
해설: 부울 곱셈은 논리곱(AND) 연산을 사용하여 행렬 곱을 수행하는 것이다. 주어진 행렬 A와 B는 각각 $\begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix}$와 $\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \end{pmatrix}$이다. 이 두 행렬의 부울곱을 계산하면 $\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix}$가 된다. 따라서 정답은 2번이다. 다른 선택지들은 부울곱의 결과가 아니다.
6강. 관계
1. 집합 A={1,2,3,4}, B={3.4}일 때, R={(a,b)|a+b=5}로 옳은 것은?
1 3 R3이 성립한다.
2 4 R4이 성립한다.
3 2 R3이 성립하지 않는다.
4) 1 R4이 성립한다.
정답: 4
해설: 관계 \( R \)은 \( a + b = 5 \)를 만족하는 \((a, b)\) 쌍으로 구성된다. 선택지 1에서 3 + 3 = 6으로 성립하지 않고, 선택지 2에서 4 + 4 = 8로 성립하지 않는다. 선택지 3에서 2 + 3 = 5로 \( 2R3 \)이 성립하므로 잘못된 설명이다. 선택지 4에서 1 + 4 = 5로 \( 1R4 \)이 성립하여 옳다. 따라서 정답은 4번이다.
2. 집합 A={1.2.3.4,5}, B={3.4,5}일 때, R={(a,b)|a+b=7}로 옳은 것은?
1) R={(2,3),(2,4),(2,5)}
2) R={(1,3),(2,4),(3,5)}
3) R={(2,5),(3,4),(4,3)}
4) R={(1,3),(1,4),(1,5)}
정답: 3
해설: 집합 A와 B의 원소로 구성된 순서쌍 (a, b)가 관계 \( R = \{(a, b) \mid a + b = 7\} \)를 만족하려면 a와 b의 합이 7이어야 한다. 각 선택지를 검토해보면, 1번은 \(2+3\neq7\), \(2+4\neq7\), \(2+5\neq7\)로 틀리다. 2번은 \(1+3\neq7\), \(2+4\neq7\), \(3+5=8\)로 모두 틀리다. 4번은 \(1+3\neq7\), \(1+4\neq7\), \(1+5\neq7\)로 틀리다. 3번은 \(2+5=7\), \(3+4=7\), \(4+3=7\)로 모든 조건을 만족한다. 따라서 정답은 3번이다.
3. X={1,2,3,4,5}에서 관계 R이 다음과 같을 때, 관계 R에 대해 옳은 것은?
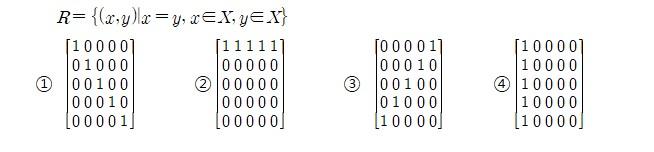
1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 관계 \(R = \{(x, y) \mid x = y, x \in X, y \in X\}\)는 동일한 원소 쌍들로 이루어져 있어야 한다. 이는 대각선에만 1이 있는 항등 관계를 나타낸다. ①번 행렬은 대각선 원소가 모두 1이고 나머지 원소가 모두 0이므로 조건을 만족한다. ②번은 모든 원소가 1이어서 잘못되었고, ③번과 ④번은 대각선 외의 위치에 1이 있어 조건을 만족하지 않는다. 따라서 정답은 1번이다.
4. 위 지문에서 관계의 성질에 대해 잘못 설명한 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 관계의 반사성, 대칭성, 추이성에 대한 설명은 맞다. ①번은 모든 \(a \in A\)에 대해 \(aRa\)가 성립하면 반사적 관계이다. ②번은 \(aRb\)이면 \(bRa\)가 성립하는 경우 대칭적 관계이다. ③번은 \(aRb\)이고 \(bRc\)이면 \(aRc\)가 성립하면 추이적 관계이다. 그러나 ④번에서 \(aRb \lor bRc \rightarrow aRc\)는 반사적 관계가 아니라 이행적 관계를 잘못 설명한 것이다. 따라서 잘못된 설명은 ④번이다.
5. A에서 B로의 관계일 때, R의 역관계 R ‐ ¹ 으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 2
해설: 관계 R의 역관계 \(R^{-1}\)는 R에 있는 각 쌍의 순서를 바꾼 것이다. R={(1,b), (3,c), (4,d), (3,d), (2,a)}에서 각 쌍을 뒤집으면 {(b,1), (c,3), (d,4), (d,3), (a,2)}가 된다. 이를 선택지와 비교하면, ②번이 정확히 매칭된다. ①번, ③번, ④번은 쌍의 순서가 맞지 않거나 잘못된 쌍이 포함되어 있다. 따라서 올바른 역관계는 ②번이다.
6. 다음 관계에 대한 설명으로 옳은 것은?

1) 반사적이 아니다
2) 추이적이 아니다
3) 대칭적이다
4) 반사적이다
정답: 4
해설: 주어진 그래프는 각 노드에 대한 자기 자신으로의 간선(루프)을 가지고 있으므로 반사적이다. 반사적 관계는 모든 노드 \(a\)에 대해 \(aRa\)가 성립하는 것을 의미한다. 그래프를 보면 모든 노드(1, 2, 3)에 자기 자신으로의 간선이 존재한다. 반면, 대칭적 관계는 \(aRb\)일 때 \(bRa\)도 성립해야 하는데, 1에서 2로 가는 간선이 있지만 2에서 1로 가는 간선이 없으므로 대칭적이지 않다. 또한 1에서 3으로 가는 경로가 2를 통해 존재하므로 추이적이다. 따라서 옳은 설명은 반사적이다.
7. 다음 관계에 대한 설명으로 옳지 않은 것은?

1) 반사적이 아니다
2) 추이적이다
3) 대칭적이다
4) 대칭적이 아니다
정답: 3
해설: 주어진 그래프를 보면 노드 1, 2, 3 중 자기 자신으로 돌아오는 루프가 없으므로 반사적이지 않다. 대칭적 관계는 \(aRb\)일 때 \(bRa\)도 성립해야 하는데, 노드 1에서 2로 가는 간선이 있지만, 2에서 1로 가는 간선이 없으므로 대칭적이지 않다. 또한 1에서 3으로 가는 경로가 있지만, 3에서 1로 가는 경로가 없기 때문에 대칭적이지 않다. 추이성은 직접적으로 확인할 수 없지만, 대칭적이지 않다는 것은 명백하다. 따라서 옳지 않은 설명은 3번이다.
8. 집합 A = { 1, 2, 3, 4, 5, 6 } 와 집합 B = { a, b, c, d }이고 A 에서 B 로의 관계 R 과 B 에서 A 로의 관계 S 가 다음과 같을 때, 합성 관계 S · R 으로서 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 합성 관계 \( S \cdot R \)는 관계 R에서 출발해서 관계 S로 도착하는 쌍을 찾는 것이다. R={(1,b), (2,c), (3,d), (4,a)}와 S={(a,3), (b,4), (c,5), (d,6)}에서 R의 각 원소를 S에 대입하면, (1,b) -> (b,4) -> (1,4), (2,c) -> (c,5) -> (2,5), (3,d) -> (d,6) -> (3,6), (4,a) -> (a,3) -> (4,3)가 된다. 따라서 \( S \cdot R \)은 {(1,4), (2,5), (3,6), (4,3)}로, 이는 ①번과 일치한다. 나머지 선택지는 관계를 잘못 합성한 결과이다.
9. 동치에 대한 설명으로 옳은 것은?
1) 집합 A에 대한 관계 R이 있을 때, R이 반사적, 대칭적, 추이적이지 않으면 R은 동치관계이다.
2) 집합 A에 대한 관계 R이 있을 때, R이 반사적, 대칭적, 추이적이면 R은 동치관계이다.
3) 집합 A에 대한 관계 R이 있을 때, R이 반사적이며, 대칭적이지 않으며, 추이적이면 R은 동치관계이다.
4) 집합 A에 대한 관계 R이 있을 때, R이 반사적이지 않으며, 대칭적, 추이적이면 R은 동치관계이다.
정답: 2
해설: 동치관계는 반사적, 대칭적, 추이적 성질을 모두 만족하는 관계이다. 1번은 반사적, 대칭적, 추이적이지 않으면 동치관계가 아니므로 틀리다. 3번은 반사적이고 추이적이지만 대칭적이지 않으면 동치관계가 아니므로 틀리다. 4번은 반사적이지 않으면 동치관계가 아니므로 틀리다. 따라서 반사적, 대칭적, 추이적 성질을 모두 만족하는 2번이 옳다.
10. 다음 부울행렬에 대한 설명으로 옳은 것은?

1) 반사적, 대칭적이다.
2) 대칭적, 추이적이다.
3) 반사적, 추이적이다.
4) 반사적이 아니고, 추이적이 아니다.
정답: 1
해설: 부울행렬이 반사적이려면 모든 대각 원소가 1이어야 한다. 주어진 행렬의 대각 원소는 모두 1이므로 반사적이다. 대칭적이려면 행렬의 전치 행렬이 원래 행렬과 같아야 한다. 주어진 행렬을 전치하면 원래 행렬과 동일하므로 대칭적이다. 따라서 이 행렬은 반사적이고 대칭적이다. 2번은 이 행렬이 추이적이지 않으므로 틀리다. 3번과 4번은 반사적이고 대칭적인 성질에 맞지 않아 부적절하다.
돌발 1. A = { 1, 2, 3 }일 때, 다음 방향그래프가 표현하고 있는 관계 R로서 옳은 것은?

1) R = { ( 1, 1 ), ( 2, 2 ), ( 3, 3 ) }
2) R = { ( 1, 2 ), ( 2, 1 ), ( 3, 1 ), ( 3, 2 ) }
3) R = { ( 1, 1 ), ( 1, 2 ), ( 2, 1 ), ( 2, 2 ), ( 3, 1 ), ( 3, 2 ) }
4) R = { ( 1, 1 ), ( 1, 2 ), ( 2, 1 ), ( 2, 2 ), ( 3, 1 ), ( 3, 2 ) , ( 3, 3 ) }
정답: 3
해설: 주어진 방향 그래프는 정점 1, 2, 3과 그들 사이의 관계를 나타낸다. 자기 자신으로 돌아가는 루프가 있는 정점은 1과 2이며, 이는 (1, 1)과 (2, 2)에 해당한다. 또한, 1에서 2로, 2에서 1로, 3에서 1로, 3에서 2로 가는 간선이 있으므로 (1, 2), (2, 1), (3, 1), (3, 2)가 포함된다. 따라서 관계 R은 (1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2)로 구성된다. 선택지 4번은 (3, 3)이 포함되어 잘못되었고, 선택지 1번과 2번은 필요한 관계가 부족하다.
7강. 함수
1. A = {1, 2. 3}, B = {a, b, c, d, e} 일 때, A 에서 B 로의 함수인 것은?
1) R = { ( 1, a ), ( 1, b ), ( 2, c ), ( 3, d ), ( 3, e ) }
2) R = { ( 1, b ), ( 2, c ), ( 3, d ), ( 3, e ) }
3) R = { ( 1, c ), ( 2, b ), ( 2, c ), ( 3, e ) }
4) R = { ( 1, a ), ( 2, b ), ( 3, c ) }
정답: 4
해설: 함수는 A의 각 원소가 B의 유일한 원소와 대응해야 한다. 선택지 1번은 1과 3이 각각 두 개의 원소와 대응하므로 함수가 아니다. 선택지 2번도 3이 두 개의 원소와 대응하므로 함수가 아니다. 선택지 3번은 2가 두 개의 원소와 대응하므로 함수가 아니다. 선택지 4번은 A의 모든 원소가 B의 유일한 원소와 대응하므로 함수이다. 따라서 정답은 4번이다.
2. A = {1, 2. 3}, B = {4, 5, 6} 일 때, A 에서 B 로의 함수 R = { (1, 5), (2, 4), (3, 6) } 에 대해 다음 설명 중 옳은 것은?
1) R 의 정의역은 { 4, 5, 6 } 이다.
2) R 의 공역과 치역은 같다.
3) 원소 1 의 상은 4 이다.
4) R 의 치역은 {1, 2, 3} 이다.
정답: 2
해설: 주어진 함수 \( R \)에서 정의역은 함수의 첫 번째 원소 집합이므로 \{1, 2, 3\}이다. 공역은 B이므로 \{4, 5, 6\}이고, R의 치역은 실제로 대응되는 값의 집합이므로 \{4, 5, 6\}이다. 따라서 공역과 치역은 같다. 선택지 1번은 정의역을 잘못 정의하였고, 선택지 3번은 원소 1의 상이 5임에도 4로 잘못 기술하였다. 선택지 4번은 치역을 잘못 설명하고 있다.
3. A = {1, 2, 3, 4} 일 때, 다음 관계 중에서 역함수를 가지는 함수는 어느 것인가?
1) R = { ( 1, 2 ), ( 2, 1 ), ( 3, 4 ), ( 4, 3 ) }
2) R = { ( 1, 2 ), ( 2, 1 ), ( 3, 3 ), ( 3, 4 ) }
3) R = { ( 1, 1 ), ( 2, 2 ), ( 3, 3 ) }
4) R = { ( 2, 1 ), ( 1, 2 ), ( 3, 4 ) }
정답: 1
해설: 정답은 1이다. 함수가 역함수를 가지기 위해서는 일대일 대응이어야 한다. 선택지 1의 경우, 모든 원소가 정확히 하나의 쌍으로 매칭되어 있으며, 각 쌍의 관계를 뒤집으면 원래 함수가 되므로 역함수가 존재한다. 반면에 선택지 2는 (3, 3)과 (3, 4)처럼 같은 원소가 두 번 나오므로 일대일 대응이 아니고, 선택지 3은 (4, 4)와 같은 쌍이 없어서 정의역과 공역이 일대일 대응이 아니다. 선택지 4는 (2, 1)과 (1, 2)가 서로 바뀌긴 했지만 (3, 4)의 역함수가 (4, 3)으로 매칭되지 않아서 역함수를 가지지 않는다.
4. 두 함수 ⨍ : Z→Z, ɡ : Z→Z 가 ⨍(x) = 2x + 2, ɡ(x) = 3x + 1 일 때, 합성함수 ɡ ∘ ⨍ 에 대한 것으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 합성함수 \( (g \circ f)(x) \)는 \( g(f(x)) \)로 정의된다. 여기서 \( f(x) = 2x + 2 \)이고 \( g(x) = 3x + 1 \)이므로, \( g(f(x)) = g(2x + 2) = 3(2x + 2) + 1 = 6x + 6 + 1 = 6x + 7 \)이다. 따라서 합성함수 \( g \circ f \)는 \( 6x + 7 \)이므로 정답은 4번이다. 선택지 1번, 2번, 3번은 각각 \( 6x^2 + 8x + 2 \), \( 6x + 4 \), \( 5x + 3 \)로, 올바른 합성함수 결과가 아니다.
5. 두 함수 ⨍ : Z→Z, ɡ : Z→Z 가 ⨍(x) = 2x , ɡ(x) = 2x + 3 일 때, 합성함수 ⨍ ∘ ɡ 에 대한 것으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 합성함수 \( (f \circ g)(x) \)는 \( f(g(x)) \)로 정의된다. 여기서 \( f(x) = 2x \)이고 \( g(x) = 2x + 3 \)이므로, \( f(g(x)) = f(2x + 3) = 2(2x + 3) = 4x + 6 \)이다. 따라서 합성함수 \( f \circ g \)는 \( 4x + 6 \)이므로 정답은 3번이다. 선택지 1번, 2번, 4번은 각각 \( 4x^2 + 6x \), \( 4x + 3 \), \( 4x^2 + 3 \)로, 올바른 합성함수 결과가 아니다.
6. 다음에 대해 옳은 것은?
1) 0 ! = 0
2) 1 ! = 1
3) 2 ! = 3
4) 4 ! = 36
정답: 2
해설: 1번은 0! = 1이므로 잘못되었다. 2번은 1! = 1로 옳다. 3번은 2! = 2 \times 1 = 2이므로 잘못되었다. 4번은 4! = 4 \times 3 \times 2 \times 1 = 24이므로 잘못되었다. 따라서 정답은 2번이다.
c.f. 0!는 1이다. 이는 수학적 정의와 조합론적 이유에서 비롯된다. 팩토리얼의 정의에 따르면, n!는 n부터 1까지의 모든 자연수의 곱이다. 특별히, 0!는 빈 곱으로 간주되어 1로 정의된다. 조합론적으로, 0개의 항목을 고르는 경우의 수는 1가지이기 때문에 0! = 1로 정의된다.
7. 수식을 간단히 표현한 것으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: ① 번은 $ \frac{7!}{5!} = \frac{7 \times 6 \times 5!}{5!} = 7 \times 6 = 42$로 옳다. ② 번은 $\frac{(n-2)!}{n!} = \frac{1}{n(n-1)}$로 $(n-1)/n$과 같지 않다. ③ 번은 $\frac{4!}{3!} = \frac{4 \times 3!}{3!} = 4$로 3이 아니다. ④ 번은 $\frac{n!}{(n-1)!} = \frac{n \times (n-1)!}{(n-1)!} = n$으로 $(n-1)$이 아니다. 따라서 옳은 것은 ① 번이다.
8. 다음 지문에 대한 값으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: $\frac{5!}{6!}$는 $\frac{5!}{6 \times 5!} = \frac{1}{6}$이다. 따라서 옳은 값은 3번인 $\frac{1}{6}$이다. 1번은 6으로, 2번은 5로, 4번은 $\frac{1}{6!}$로 모두 잘못된 값이다. 정답은 3번이다.
9. 다음 함수의 값으로 옳지 않은 것은?
1) ⌊ 3.2 ⌋ = 3
2) ⌈ 4.2 ⌉ = 5
3) ⌊ − 0.5 ⌋ = − 1
4) ⌈ − 1.5 ⌉ = − 2
정답: 4
해설: 바닥 함수(⌊x⌋)와 천장 함수(⌈x⌉)의 정의에 따라 각 선택지의 값을 계산하면 된다. 바닥 함수는 x보다 작거나 같은 최대 정수를 반환하고, 천장 함수는 x보다 크거나 같은 최소 정수를 반환한다. 1번 선택지는 ⌊3.2⌋ = 3으로 맞다. 2번 선택지는 ⌈4.2⌉ = 5로 맞다. 3번 선택지는 ⌊−0.5⌋ = −1로 맞다. 4번 선택지는 ⌈−1.5⌉ = −1이 되어야 하므로 틀리다. 선택지 4번의 값이 −2가 아니라 −1이므로 정답이다.
10. 다음 함수의 값으로 옳은 것은?
1) 7 mod 3 = 2
2) 7 mod (−2) = − 1
3) 3 mod 3 = 1
4) 4 mod 7 = 0
정답: 2
해설: 공식 \( n \mod m = n - m \left\lfloor \frac{n}{m} \right\rfloor \)을 사용하여 \( 7 \mod (-2) \)를 계산하면, 먼저 \( \left\lfloor \frac{7}{-2} \right\rfloor \)를 구해야 한다. \( \frac{7}{-2} \)는 -3.5이므로 내림하여 -4가 된다. 따라서 \( 7 - (-2) \times (-4) = 7 - 8 = -1 \)이다. 선택지 1번은 7 mod 3 = 1, 선택지 3번은 3 mod 3 = 0, 선택지 4번은 4 mod 7 = 4이다. 따라서 정답은 2번이다.
돌발 1. A = { 1, 2. 3 }, B = { a, b, c, d } 일 때, 다음 관계 중 함수를 고르시오.
1) R = { ( 1, a ), ( 2, b ) }
2) R = { ( 1, a ), ( 2, a ), ( 3, b ) }
3) R = { ( 1, a ), ( 2, a ), ( 3, e ) }
4) R = { ( 1, a ), ( 2, a ), ( 3, b ), ( 3, d ) }
정답: 2
해설: 함수는 집합 A의 각 원소가 집합 B의 유일한 원소와 대응되어야 한다. 1번 선택지는 1, 2만 있고 3이 없으므로 함수가 아니다. 3번 선택지는 B에 없는 원소 e가 포함되어 함수가 아니다. 4번 선택지는 3이 B의 두 원소 b와 d에 대응되어 있으므로 함수가 아니다. 2번 선택지는 집합 A의 각 원소가 집합 B의 유일한 원소와 대응되므로 함수이다.
8강. 부울대수
1. 다음 진리표에 해당되는 논리게이트로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 2
해설: 주어진 진리표에서 \( x \)와 \( y \)의 조합에 따른 \( f \)의 값을 보면, \( x = 0 \)이고 \( y = 0 \)일 때 \( f = 1 \), 그 외의 경우에는 \( f = 0 \)이다. 이는 NOR 게이트의 특성과 일치한다. NOR 게이트는 입력이 모두 0일 때 출력이 1이고, 그 외의 경우에는 출력이 0이다. 선택지 1번은 AND 게이트, 3번은 OR 게이트, 4번은 NAND 게이트로, 모두 진리표와 일치하지 않는다. 따라서 정답은 2번이다.
2. 다음 설명에 해당되는 논리게이트로 옳은 것은?
X와 Y의 입력이 들어왔을 때,
X의 값이 1, Y의 값이 1일 때를 제외한 모든 출력 값으로 1을 갖는 논리게이트
1) XOR
2) NOR
3) 버퍼
4) NAND
정답: 4
해설: NAND 게이트는 두 입력이 모두 1일 때만 출력이 0이 되고, 나머지 경우에는 모두 출력이 1이 된다. 이는 X와 Y가 모두 1일 때를 제외한 모든 경우에 출력이 1이 되는 조건을 만족한다. XOR 게이트는 두 입력이 다를 때만 1을 출력하므로 적절하지 않다. NOR 게이트는 두 입력이 모두 0일 때만 1을 출력하므로 조건에 맞지 않는다. 버퍼는 입력을 그대로 출력하므로 논리 연산을 수행하지 않는다. 따라서 정답은 4번 NAND이다.
3. 부울식에 대한 설명으로 옳지 않은 것은?
1) 상수 0, 1은 부울식이다.
2) 부울변수는 부울식이다.
3) X, Y가 부울식일 때, X+Y도 부울식이다.
4) X, Y가 부울식일 때, 2X+3Y도 부울식이다.
정답: 4
해설: 부울식은 논리적인 참(True)과 거짓(False) 값을 가지는 식을 의미한다. 상수 0과 1은 부울식이며, 부울변수 역시 부울식이다. 또한, X와 Y가 부울식일 때, X+Y는 논리적 OR을 의미하므로 부울식이다. 하지만 2X+3Y는 부울식이 아니다. 부울식에서는 상수 계수를 곱하는 산술 연산이 허용되지 않기 때문이다.
4. 부울대수의 기본 정리 중에서 올바른 것은?
1) X • 1 = X
2) X + 1 = X
3) X • 0 = X
4) X • X = 2X
정답: 1
해설: 부울대수의 기본 정리 중 올바른 것은 X • 1 = X이다. 이는 논리곱에서 항등법칙에 해당한다. 2번 X + 1 = X는 논리합에서의 항등식이 아니고, 3번 X • 0 = X는 논리곱의 소멸 법칙에 위배되며, 4번 X • X = 2X는 부울대수에서 정의되지 않는 잘못된 표현이다. 따라서 정답은 1번이다.
5. 부울대수의 기본 정리 중에서 올바른 것은?

1) 1
2) 2
3) 3
4) 4
정답: 1
해설: X + Y = Y + X는 교환법칙으로 부울대수의 기본 정리에 해당한다. 2번 X + X • Y = X는 드모르간의 정리가 아니며, 3번 X • (X + Y) = X는 결합법칙이 아니라 흡수법칙이다. 4번 XY = YX는 교환법칙이다. 따라서 올바른 정리는 1번이다.
6. 부울대수의 기본 정리 중에서 올바르지 않은 것은?

1) 1
2) 2
3) 3
4) 4
정답: 3
해설: 부울대수의 기본 정리 중에서 3번 X \cdot \overline{X} = 1은 잘못된 식이다. X와 \overline{X}는 상보 관계로, 둘을 AND 연산하면 항상 0이 된다. 따라서 X \cdot \overline{X} = 0이어야 한다. 1번 \overline{\overline{X}} = X는 이중 부정 법칙이고, 2번 X + X = X는 흡수 법칙이다. 4번 X + YZ = (X + Y)(X + Z)는 분배 법칙이다. 따라서 3번이 올바르지 않은 정리이다.
7. 다음 지문에 제시된 부울함수의 보수로 올바른 것은?

1) 1
2) 2
3) 3
4) 4
정답: 4
해설: 부울 함수 \( F = \overline{XYZ} + XY\overline{Z} \)의 보수를 구하려면 드모르간 법칙과 보수 법칙을 사용해야 한다. 드모르간 법칙에 따르면, \( \overline{A + B} = \overline{A} \cdot \overline{B} \)와 \( \overline{A \cdot B} = \overline{A} + \overline{B} \)가 성립한다. 따라서 \( F \)의 보수는 \( \overline{\overline{XYZ} + XY\overline{Z}} = (\overline{\overline{XYZ}}) \cdot (\overline{XY\overline{Z}}) \)가 된다. 이를 전개하면 \( (X + \overline{Y} + Z) \cdot (\overline{X} + \overline{Y} + Z) \)가 된다. 따라서 정답은 4번이다. 선택지 1, 2, 3번은 부울 함수의 보수를 올바르게 표현하지 않았다.
8. 다음 부울대수식 F = ( X + X Y + Y ) • ( X + X Y ) 을 최대한 간소화 한 것은?
1) F = X + X Y
2) F = X
3) F = Y
4) F = X X + X Y
정답: 2
해설: 주어진 부울 대수식 \( F = (X + XY + Y) \cdot (X + XY) \)를 간소화하면 다음과 같다. 먼저 \( X + XY = X \)로 흡수 법칙을 적용할 수 있다. 따라서 \( F = (X + XY + Y) \cdot X \)가 된다. \( X + XY = X \)이고, \( X + Y = X + Y \)이므로, 다시 \( F = (X + Y) \cdot X \)가 된다. 분배 법칙을 적용하면 \( F = X \cdot X + Y \cdot X = X \)가 된다. 따라서 정답은 2번이다. 선택지 1, 3, 4는 올바른 간소화 결과가 아니다.
9. 다음 부울대수식을 간소화하는 과정 중 빈 칸에 들어갈 수식으로 옳은 것은?

1) 1
2) 2
3) 3
4) 4
정답: 3
해설: 주어진 부울 대수식 \( F = (X + \overline{Y})(X + Z) \)를 전개하고 간소화하는 과정에서 빈 칸에 들어갈 수식을 구하자. 전개하면 \( XX + XZ + \overline{Y}X + \overline{Y}Z \)가 된다. \( XX \)는 \( X \)로 간소화되고, \( XZ + \overline{Y}X + \overline{Y}Z \)를 정리하면 \( X(1 + Z + \overline{Y}) + \overline{Y}Z \)가 된다. 여기서 \( 1 + Z + \overline{Y} \)는 항상 1이므로, 이 부분은 \( X \cdot 1 + \overline{Y}Z \)가 된다. 따라서 빈 칸에 들어갈 수식은 \( X \cdot 1 + \overline{Y}Z \)이다. 선택지 3번이 이에 해당한다. 다른 선택지는 간소화 과정에 적합하지 않다.
10. 다음 부울대수식을 간소화한 결과로 옳은 것은?

1) 1
2) 2
3) 3
4) 4
정답: 3
해설: 주어진 부울 대수식 \(ABC + AB\overline{C} + A\overline{B}C\)를 간소화하면 다음과 같다. 먼저 공통된 인수 \(A\)를 묶어내면, \(A(BC + B\overline{C} + \overline{B}C)\)가 된다. 식 내부를 다시 정리하면, \(B(C + \overline{C}) + \overline{B}C\)가 되고, 이는 \(B \cdot 1 + \overline{B}C\)로 단순화된다. 따라서 최종 간소화된 식은 \(A(B + C)\)가 된다. 이를 다시 정리하면 \(AB + AC\)가 되므로, 정답은 3번이다. 다른 선택지는 주어진 부울 대수식을 올바르게 간소화하지 않았다.
돌발 1. 다음 진리표에 해당하는 논리게이트를 선택하세요.

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 주어진 진리표에서 X와 Y의 입력에 따른 출력 F를 보면, (0, 0)일 때 0, (0, 1)일 때 1, (1, 0)일 때 1, (1, 1)일 때 0이 된다. 이는 XOR 게이트의 출력과 일치한다. XOR 게이트는 두 입력이 다를 때 1을 출력하고, 같을 때 0을 출력하는 특성을 가진다. 1번 AND 게이트는 두 입력이 모두 1일 때만 1을 출력하므로 적합하지 않다. 2번 OR 게이트는 입력 중 하나라도 1일 때 1을 출력하므로 적합하지 않다. 3번 NAND 게이트는 두 입력이 모두 1일 때만 0을 출력하므로 적합하지 않다. 따라서 정답은 4번 XOR 게이트이다.
돌발 2. 다음 중 부울함수 F = X 와 동치가 아닌 것은?
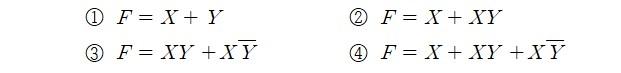
1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 부울함수 F = X와 동치가 아닌 것은 ①번이다. ① F = X + Y는 X와 Y의 값에 따라 다른 값을 가질 수 있으므로 X와 동치가 아니다. ② F = X + XY는 분배법칙에 의해 F = X가 된다. ③ F = XY + X(이거나 Y)는 드모르간의 법칙에 의해 F = X가 된다. ④ F = X + XY + X(이거나 Y)는 분배법칙에 의해 F = X가 된다. 따라서 동치가 아닌 것은 ①번이다.
9강 그래프 1
1. 그래프에 관련된 용어에 대한 설명으로 옳은 것은?
1) 동일한 꼭지점을 연결하는 변은 인접했다고 한다.
2) 두 꼭지점을 연결하는 변이 두 개 이상 있을 때 이러한 변들을 병렬 변이라 한다.
3) 어떠한 변도 연결되지 않은 그래프를 무향 그래프라 한다.
4) 어떤 루프나 어떤 병렬 변을 가지지 않는 무향 그래프를 완전 그래프라 한다.
정답: 2
해설: 그래프에서 두 꼭지점을 연결하는 변이 두 개 이상 있을 때 이러한 변들을 병렬 변이라 한다. 선택지 1번은 동일한 꼭지점을 연결하는 변은 루프라고 한다. 선택지 3번은 어떠한 변도 연결되지 않은 그래프는 비연결 그래프 또는 독립 그래프라 한다. 선택지 4번은 어떤 루프나 병렬 변을 가지지 않는 무향 그래프는 단순 그래프라 한다. 완전 그래프는 모든 꼭지점 쌍이 변으로 연결된 그래프를 의미한다.
2. 다음 그래프에 대한 설명으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 그래프에서 루프는 꼭지점에서 시작하여 다시 그 꼭지점으로 돌아오는 변을 의미한다. 그림에서 \( v_1 \)은 변 \( e_4 \)를 통해 스스로 연결되어 있으므로 루프를 가지고 있다. 선택지 1번은 고립된 꼭지점은 변이 연결되지 않은 꼭지점인데, \( v_1 \)은 변 \( e_1 \), \( e_4 \)에 연결되어 있어 고립된 꼭지점이 아니다. 선택지 2번은 \( v_3 \)와 인접한 꼭지점이 \( v_2 \)만 포함되어 있어 옳지 않다. 선택지 3번은 변 \( e_1 \)이 병렬 변이 아니라 단순 변이므로 틀렸다.
3. 다음 그래프들 중 다른 그래프 하나는?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 주어진 그래프들 중 3번 그래프는 다른 그래프와 구조가 다르다. 1번, 2번, 4번 그래프는 모두 5개의 꼭지점과 6개의 변으로 이루어진 동일한 그래프를 표현하고 있다. 이들은 모두 서로 연결된 꼭지점의 개수와 변의 개수가 동일하여 서로 동형이다. 반면 3번 그래프는 변이 하나 더 추가되어 있어 총 7개의 변을 가지고 있으며, 이는 다른 그래프와 동형이 아니므로 다른 그래프이다.
4. 다음 그래프에 대한 설명으로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 진출 차수는 꼭지점에서 나가는 변의 개수를 의미한다. \(v_1\)에서 나가는 변은 \(v_2\)와 \(v_4\)로 향하는 두 개의 변이므로 \(v_1\)의 진출 차수는 2이다. 선택지 2번은 \(v_2\)의 진입 차수가 1이므로 틀리다. 선택지 3번은 \(v_3\)의 진입 차수가 2이므로 틀리다. 선택지 4번은 \(v_4\)의 진출 차수가 1이므로 틀리다.
5. 다음 그래프에서 차수가 3인 꼭지점들을 모두 고른 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 차수는 한 꼭지점에 연결된 변의 개수를 의미한다. \(v_3\)와 \(v_4\)의 차수는 각각 3이다. \(v_3\)는 \(v_1\), \(v_2\), \(v_4\)와 연결되어 있고, \(v_4\)는 \(v_1\), \(v_3\), \(v_5\)와 연결되어 있다. 선택지 1번의 \(v_1\)은 차수가 4이고, 선택지 2번의 \(v_2\)와 \(v_3\) 중 \(v_2\)는 차수가 2이다. 선택지 4번의 \(v_3\), \(v_4\), \(v_5\) 중 \(v_5\)는 차수가 4이다. 따라서 정답은 3번이다.
6. 다음 그래프의 총 차수로 옳은 것은?

1) 35
2) 30
3) 20
4) 15
정답: 2
해설: 주어진 그래프는 10개의 꼭지점이 각 3개의 변에 연결되어 있어 각 꼭지점의 차수는 3이다. 총 차수는 모든 꼭지점의 차수의 합이므로 10개의 꼭지점에 대한 차수 합계는 \(10 \times 3 = 30\)이다. 따라서 총 차수는 30이다. 선택지 1번은 각 꼭지점의 차수를 3이 아닌 3.5로 계산한 값이다. 선택지 3번과 4번은 각각 각 꼭지점의 차수를 2와 1.5로 계산한 값이므로 옳지 않다.
7. 다음 그래프를 인접 행렬로 표현한 것 중 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 인접 행렬은 그래프의 꼭지점들 간의 연결 상태를 행렬로 표현한 것이다. 주어진 그래프에서 \(v_1\)과 \(v_2\), \(v_1\)과 \(v_4\), \(v_2\)와 \(v_3\), \(v_2\)와 \(v_4\)가 각각 연결되어 있다. \(v_3\)는 루프를 가지고 있다. 이를 바탕으로 인접 행렬을 작성하면 \(v_1\) 행과 \(v_2\) 열, \(v_1\) 행과 \(v_4\) 열, \(v_2\) 행과 \(v_3\) 열, \(v_2\) 행과 \(v_4\) 열, \(v_3\) 행과 \(v_3\) 열에 1이 들어가게 된다. 따라서 1번 선택지가 옳다. 나머지 선택지들은 그래프의 연결 상태를 정확히 반영하지 못하고 있다.
8. 다음 그래프를 발생행렬로 표현한 것 중 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 발생 행렬은 그래프의 변과 꼭지점 간의 연결 상태를 나타낸다. 주어진 그래프에서 변 \(e_1\)은 \(v_1\)과 \(v_2\)를, \(e_2\)는 \(v_2\)와 \(v_3\)를, \(e_3\)는 \(v_2\)와 \(v_4\)를, \(e_4\)는 \(v_1\)과 \(v_4\)를, \(e_5\)는 \(v_3\)와 \(v_4\)를 연결한다. 3번 발생 행렬은 각 변이 연결된 꼭지점을 정확히 나타낸다. 1번, 2번, 4번 선택지는 이러한 연결 상태를 제대로 반영하지 못하고 있다.
9. 다음 그래프에 대한 설명으로 옳은 것은?

1) 그래프는 한 개의 연결 요소를 가지고 있다.
2) 그래프는 두 개의 연결 요소를 가지고 있다.
3) 그래프는 세 개의 연결 요소를 가지고 있다.
4) 그래프는 연결 그래프이다.
정답: 2
해설: 주어진 그래프는 두 개의 연결 요소를 가지고 있다. 연결 요소는 서로 연결된 꼭지점들의 집합을 의미한다. \(v_1\), \(v_2\), \(v_3\), \(v_4\)는 서로 연결되어 하나의 연결 요소를 이루고, \(v_5\)는 다른 꼭지점들과 연결되지 않아 독립된 또 하나의 연결 요소를 이룬다. 선택지 1번과 4번은 모두 연결 요소의 개수를 잘못 나타내고 있으며, 선택지 3번은 연결 요소의 개수를 과장하여 나타내고 있다.
10. 꼭지점의 개수가 6개인 완전 그래프의 변의 개수는 몇 개인가?
1) 6개
2) 8개
3) 10개
4) 15개
정답: 4
해설: 꼭지점의 개수가 \( n \)인 완전 그래프의 변의 개수는 \( \frac{n(n-1)}{2} \)이다. \( n = 6 \)일 때 변의 개수는 \( \frac{6(6-1)}{2} = \frac{6 \cdot 5}{2} = 15 \)이다. 따라서 정답은 15개이다. 선택지 1번은 \( n = 4 \)일 때의 변의 개수이고, 선택지 2번은 \( n = 4 \)일 때의 변의 개수이며, 선택지 3번은 \( n = 5 \)일 때의 변의 개수이다.
돌발 1. 다음 그래프 G에 관한 서술로서 부적절한 것은?

1) G는 연결 그래프이다.
2) G는 완전 그래프이다.
3) G는 이분 그래프이다.
4) G는 정규 그래프이다.
정답: 3
해설: 주어진 그래프 G는 모든 정점이 서로 연결된 완전 그래프이다. 이는 모든 정점이 서로 연결되어 있어 연결 그래프이고, 모든 정점의 차수가 동일하므로 정규 그래프이다. 하지만 이분 그래프는 정점을 두 개의 분할 집합으로 나눠 같은 집합 내의 정점끼리는 연결되지 않는 그래프를 의미한다. 주어진 그래프는 모든 정점이 서로 연결되어 있어 이분 그래프가 아니다. 따라서 부적절한 서술은 3번이다.
10강. 그래프 2
1. 다음 그래프에서 평면 그래프가 아닌 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 평면 그래프는 그래프의 모든 변이 교차하지 않고 평면에 그릴 수 있는 그래프를 의미한다. ①, ②, ③ 그래프는 모두 평면에 그릴 수 있는 반면, ④ 그래프는 변들이 교차하여 평면에 그릴 수 없다. ④ 그래프는 완전 이분 그래프 \( K_{3,3} \)로서, 이는 평면 그래프가 될 수 없다. 따라서 평면 그래프가 아닌 것은 4번이다.
2. 어떤 연결된 평면 그래프가 꼭지점이 5개, 변이 6개가 있을 때 면의 수는 몇 개인가?
1) 3개
2) 4개
3) 5개
4) 6개
정답: 1
해설: 연결된 평면 그래프의 면의 수를 구하기 위해서는 오일러의 다면체 정리를 사용한다. 오일러의 다면체 정리에 따르면, 꼭지점 수(V) - 변 수(E) + 면 수(F)는 항상 2이다. 이 문제에서는 V=5, E=6이므로, 5 - 6 + F = 2를 풀면 F = 3이 된다. 따라서 면의 수는 3개이다. 다른 선택지인 4개, 5개, 6개는 이 공식에 부합하지 않는다.
3. 오일러 투어에 대한 설명으로 옳은 것은?
1) 주어진 그래프가 오일러 투어를 가진다면, 해당 그래프의 모든 꼭지점의 차수는 홀수이다.
2) 모든 변을 정확히 한 번씩만 지나가고, 시작점과 종점이 동일하면 오일러 투어라 한다.
3) 주어진 그래프가 연결 그래프이고 모든 꼭지점의 차수가 홀수라면, 해당 그래프는 오일러 투어를 가진다.
4) 오일러 트레일은 오일러 투어이지만, 오일러 투어라고 해서 반드시 오일러 트레일이 되는 것은 아니다.
정답: 2
해설: 오일러 투어는 모든 변을 정확히 한 번씩 지나가며 시작점과 종점이 동일한 경로를 말한다. 1번은 잘못된 설명으로, 오일러 투어를 가지려면 모든 꼭지점의 차수는 짝수여야 한다. 3번도 틀린 설명으로, 모든 꼭지점의 차수가 홀수인 경우 오일러 투어가 아니라 오일러 경로를 가질 수 있다. 4번은 틀린 설명으로, 오일러 투어는 오일러 트레일의 특별한 경우이며, 오일러 트레일이 오일러 투어가 되는 조건은 시작점과 종점이 동일해야 한다.
4. 그래프에서 해밀턴 경로와 해밀턴 사이클에 대한 설명으로 잘못된 것은?
1) 모든 꼭지점을 한 번씩만 지나는 경로를 해밀턴 경로라 한다.
2) 시작점과 종점이 같은 해밀턴 경로를 해밀턴 사이클이라고 한다.
3) 해밀턴 경로가 존재하면, 해밀턴 사이클이 존재한다.
4) 해밀턴 사이클이 존재하면, 해밀턴 경로가 존재한다.
정답: 3
해설: 해밀턴 경로는 모든 꼭지점을 한 번씩만 지나며 시작점과 종점이 다를 수 있다. 해밀턴 사이클은 해밀턴 경로의 특별한 형태로, 시작점과 종점이 같은 경우이다. 해밀턴 경로가 존재한다고 해서 해밀턴 사이클이 반드시 존재하는 것은 아니다. 해밀턴 사이클이 존재하면 그 사이클의 한 부분 경로로 해밀턴 경로가 존재할 수 있으므로 선택지 4번은 맞다. 선택지 1번과 2번은 각각 해밀턴 경로와 해밀턴 사이클의 정의를 정확하게 설명하고 있다.
5. 다음 그래프의 오일러 투어로서 옳은 것은?

1) abcdefgh
2) cehgfdab
3) dfghecb
4) fghefghedabc
정답: 2
해설: 오일러 투어는 모든 간선을 정확히 한 번씩 지나면서 출발점으로 돌아오는 경로이다. 선택지 2) cehgfdab는 모든 간선을 한 번씩 지나고 시작점인 c로 돌아오기 때문에 오일러 투어이다. 선택지 1) abcdefgh는 b에서 h로 가는 간선이 없어 잘못되었다. 선택지 3) dfghecb는 e에서 b로 가는 간선이 없어 잘못되었다. 선택지 4) fghefghedabc는 모든 간선을 한 번씩 지나지 않으므로 오일러 투어가 아니다.
6. 다음 그래프의 해밀턴 사이클로 옳은 것은?

1) abcdef
2) abdcefa
3) abcdfea
4) afebac
정답: 2
해설: 해밀턴 사이클은 모든 정점을 한 번씩만 지나며 시작점으로 돌아오는 경로이다. 선택지 2) abdcefa는 모든 정점을 한 번씩 방문하고 시작점인 a로 돌아오기 때문에 해밀턴 사이클이다. 선택지 1) abcdef는 f에서 a로 가는 간선이 없어서 잘못되었다. 선택지 3) abcdfea는 e와 f를 두 번 방문하기 때문에 해밀턴 사이클이 아니다. 선택지 4) afebac는 c에서 시작점으로 돌아가지 않아 잘못되었다.
7. 다음 그래프의 해밀턴 사이클로 틀린 것은?

1) abcda
2) bdcab
3) cbdac
4) dabad
정답: 4
해설: 해밀턴 사이클은 모든 정점을 한 번씩 방문하고 시작점으로 돌아오는 경로이다. 선택지 4) dabad는 a와 d를 두 번 방문하기 때문에 해밀턴 사이클이 아니다. 선택지 1) abcda는 모든 정점을 한 번씩 방문하고 시작점으로 돌아오므로 해밀턴 사이클이다. 선택지 2) bdcab도 모든 정점을 한 번씩 방문하고 시작점으로 돌아오므로 해밀턴 사이클이다. 선택지 3) cbdac 역시 모든 정점을 한 번씩 방문하고 시작점으로 돌아오므로 해밀턴 사이클이다.
8. 다음 그래프에 관한 설명으로 적절한 것은?

1) 오일러 투어는 없으며, 해밀턴 사이클은 존재한다.
2) 오일러 투어는 존재하고, 해밀턴 사이클은 존재하지 않는다.
3) 오일러 투어와 해밀턴 사이클이 모두 존재한다.
4) 오일러 투어와 해밀턴 사이클이 모두 존재하지 않는다.
정답: 1
해설: 오일러 투어는 모든 간선을 한 번씩만 지나면서 출발점으로 돌아오는 경로로, 모든 정점의 차수가 짝수여야 존재한다. 주어진 그래프에서는 홀수 차수의 정점이 있으므로 오일러 투어는 없다. 반면, 해밀턴 사이클은 모든 정점을 한 번씩만 지나면서 출발점으로 돌아오는 경로로, 주어진 그래프에서는 이를 만족하는 경로가 존재한다. 따라서 오일러 투어는 없고, 해밀턴 사이클은 존재한다. 선택지 2, 3, 4는 각각 조건을 만족하지 않는다.
9. 다음 그래프에서 해밀턴 사이클로서 옳게 표현된 것은?

1)

2)

3)

4)

정답: 3
10. 다음 그래프에서 데이크스트라 알고리즘을 이용하여 꼭지점 에서 다른 꼭지점까지의 최단경로를 바르게 계산한 것은?

1) 𝑎에서 𝑏까지의 최단 경로는 13이다.
2) 𝑎에서 𝑐까지의 최단 경로는 10이다.
3) 𝑎에서 𝑑까지의 최단 경로는 11이다.
4) 𝑎에서 𝑒까지의 최단 경로는 8이다.
정답: 1
돌발 1. 다음 그래프 중 평면 그래프가 아닌 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 3
해설: 평면 그래프는 모든 간선이 교차하지 않고 평면에 그릴 수 있는 그래프이다. ① 번 그래프는 평면 그래프로 모든 간선을 교차하지 않게 그릴 수 있다. ② 번 그래프도 평면 그래프로 모든 간선을 교차하지 않게 그릴 수 있다. ③ 번 그래프는 완전 그래프 \( K_5 \)로, 평면 그래프로 그릴 수 없는 것으로 알려져 있다. ④ 번 그래프는 \( K_3,3 \)와 같이 보이지만 이는 간선 교차 없이 그릴 수 있다. 따라서 평면 그래프가 아닌 것은 ③ 번이다.
돌발 2. 다음 그래프 G에 대한 서술로서 부적절한 것은?

1) G = (V, E)에서 꼭지점 집합 V = { a, b, c, d, e, f}이고, 간선들의 집합 E는 원소의 개수 |E| = 9이다.
2) G에는 해밀턴 경로는 있으나 해밀턴 사이클은 없다.
3) G는 가중치 그래프이다.
4) G는 방향 그래프이다.
정답: 4
해설: 그래프 G는 방향성이 없는 간선으로 구성된 무방향 그래프이다. 선택지 1번에서 언급된 꼭지점 집합 V와 간선 집합 E의 크기 9는 맞다. 선택지 2번에서 G에는 해밀턴 경로가 존재할 수 있지만 해밀턴 사이클은 존재하지 않는다. 선택지 3번에서 그래프 G는 각 간선에 가중치가 부여된 가중치 그래프이다. 따라서 선택지 4번에서 G가 방향 그래프라는 서술은 부적절하다.
11강. 트리
1. 다음 중 트리가 아닌 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 2
2. 트리에 대한 설명으로 옳지 않은 것은?
1) 사이클이 없는 단순 연결 그래프를 트리라 한다.
2) 하나의 꼭지점으로 구성된 트리는 사소한 트리(trivial tree)라 한다.
3) 내부 노드가 없는 트리를 공백 트리(empty tree)라 한다.
4) 한 개 이상의 트리로 구성된 그래프를 포레스트(forest)라고 한다.
정답: 3
해설: 내부 노드가 없는 트리는 공백 트리(empty tree)가 아니라 잎 노드만으로 구성된 트리이다. 공백 트리는 노드가 전혀 없는 트리를 의미한다. 1번은 트리의 정의로, 사이클이 없는 단순 연결 그래프가 트리이다. 2번은 하나의 꼭지점으로 구성된 트리를 사소한 트리(trivial tree)라고 하며, 이는 맞는 설명이다. 4번은 한 개 이상의 트리로 구성된 그래프를 포레스트(forest)라고 하며, 이는 옳은 설명이다.
3. 높이가 5인 이진 트리가 가질 수 있는 최대 노드의 수는?
1) 64
2) 63
3) 62
4) 61
정답: 2
해설: 이진 트리의 높이가 $h$일 때 최대 노드 수는 $2^{h+1} - 1$로 계산된다. 높이가 5인 이진 트리의 경우 $2^{5+1} - 1 = 2^6 - 1 = 64 - 1 = 63$이므로 최대 노드 수는 63이다. 선택지 1번 64는 높이가 6일 때의 최대 노드 수를 의미하고, 선택지 3번과 4번인 62와 61은 모두 높이 5인 트리에서 가능하지 않은 값이다. 따라서, 높이가 5인 이진 트리에서 가질 수 있는 최대 노드 수는 63이다.
4. 다음 그래프들 중 완전 이진 트리인 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
5. 완전 이진 트리에서 20개의 노드를 갖는 최소 높이는?
1) 4
2) 5
3) 6
4) 7
정답: 1
해설: 완전 이진 트리의 높이 h에서 최대 노드 수는 2^(h+1) - 1이다. 높이 3일 때 최대 노드 수는 2^(3+1) - 1 = 15개이고, 높이 4일 때 최대 노드 수는 2^(4+1) - 1 = 31개이다. 따라서 20개의 노드를 갖기 위해 필요한 최소 높이는 4이다. 선택지 2번은 31개의 노드까지 가능하므로 필요 이상으로 높고, 선택지 3번과 4번은 더 높아 부적절하다.
6. 높이가 5인 포화 이진 트리에는 몇 개의 노드가 있는가?
1) 31
2) 32
3) 63
4) 64
정답: 3
해설: 포화 이진 트리는 모든 레벨이 꽉 찬 트리로, 높이가 h일 때 노드의 개수는 2^(h+1) - 1이다. 높이가 5인 포화 이진 트리는 2^(5+1) - 1 = 63개의 노드를 가진다. 선택지 1번 31은 높이 4의 포화 이진 트리에 해당하고, 선택지 2번 32와 선택지 4번 64는 포화 이진 트리의 노드 개수와 일치하지 않다.
7. 다음 설명 중 옳은 것은?
1) 높이가 2인 이진 트리의 최대 노드 개수는 8개이다.
2) 높이가 3이고 16개의 노드를 가지는 완전 이진 트리가 존재한다.
3) 16개의 노드를 가지는 이진 트리의 최소 높이는 3이다.
4) 4개의 노드를 가지는 이진 트리의 최대 높이는 3이다.
정답: 4
해설: 4개의 노드를 가지는 이진 트리의 최대 높이는 3이다. 높이가 2인 이진 트리의 최대 노드 개수는 2^3 - 1 = 7개이므로 선택지 1번은 틀리다. 높이가 3인 완전 이진 트리는 최대 2^4 - 1 = 15개의 노드를 가지므로 선택지 2번은 틀리다. 16개의 노드를 가지는 이진 트리의 최소 높이는 4이다(2^4 = 16)므로 선택지 3번은 틀리다.
8. A<B<C<D<E의 관계가 성립할 때, 다음 트리 중 이진 탐색 트리로 옳은 것은?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 2
해설: 이진 탐색 트리는 각 노드의 왼쪽 서브트리에 있는 모든 값이 해당 노드의 값보다 작고, 오른쪽 서브트리에 있는 모든 값이 해당 노드의 값보다 커야 한다. 선택지 2번의 트리는 루트 노드 C의 왼쪽에 B가, 오른쪽에 D가 있으며, B의 왼쪽에 A가, D의 오른쪽에 E가 위치해 이 조건을 만족한다. 선택지 1번은 B의 오른쪽에 E가 있어야 하는데 C가 위치해 있고, 선택지 3번은 B의 오른쪽에 C가 있어야 하는데 E가 위치해 있다. 선택지 4번은 D의 오른쪽에 E가 있어야 하는데 E가 B의 오른쪽에 위치해 있어 이진 탐색 트리 조건을 만족하지 않는다.
9. 이진 탐색 트리의 각 노드가 검색의 대상이 될 확률이 다음과 같다고 할 때, 다음 트리에서 가장 효율적인 이진 탐색 트리는 어느 것인가?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 1
해설: 이진 탐색 트리에서 효율성을 높이려면 검색 확률이 높은 노드가 트리의 상위 레벨에 위치해야 한다. 각 노드의 검색 확률은 A: 0.3, B: 0.2, C: 0.4, D: 0.1이다. 트리의 각 노드의 검색 비용은 레벨에 검색 확률을 곱한 값의 합으로 계산된다.
1) 트리 ①:
- C (0.4 * 1 = 0.4)
- B (0.2 * 2 = 0.4)
- A (0.3 * 3 = 0.9)
- D (0.1 * 2 = 0.2)
- 총 비용: 0.4 + 0.4 + 0.9 + 0.2 = 1.9
2) 트리 ②:
- C (0.4 * 1 = 0.4)
- B (0.2 * 2 = 0.4)
- A (0.3 * 3 = 0.9)
- D (0.1 * 3 = 0.3)
- 총 비용: 0.4 + 0.4 + 0.9 + 0.3 = 2.0
3) 트리 ③:
- A (0.3 * 1 = 0.3)
- B (0.2 * 2 = 0.4)
- C (0.4 * 3 = 1.2)
- D (0.1 * 3 = 0.3)
- 총 비용: 0.3 + 0.4 + 1.2 + 0.3 = 2.2
4) 트리 ④:
- D (0.1 * 1 = 0.1)
- A (0.3 * 2 = 0.6)
- C (0.4 * 2 = 0.8)
- B (0.2 * 3 = 0.6)
- 총 비용: 0.1 + 0.6 + 0.8 + 0.6 = 2.1
따라서 트리 ①이 가장 낮은 총 비용(1.9)을 가지므로 가장 효율적인 이진 탐색 트리이다.
10. 다음 설명 중 잘못된 것은?
1) 그래프 G의 모든 꼭지점을 연결하고 사이클이 존재하지 않는 G의 부분 그래프를 신장 트리라고 부른다.
2) 그래프 G의 신장 트리 중에서 가장 작은 총 가중치를 가지는 트리를 G의 최소 신장 트리라고 부른다.
3) 크루스칼(Kruscal) 알고리즘은 주어진 그래프에서 가중치가 가장 작은 변부터 차례대로 트리에 추가함으로써 최소 신장 트리를 찾는 알고리즘이다.
4) 프림(Prim) 알고리즘은 주어진 그래프에서 가중치가 가장 큰 꼭지점부터 차례대로 트리에 추가함으로써 최소 신장 트리를 찾는 알고리즘이다.
정답: 4
해설: 프림(Prim) 알고리즘은 가중치가 가장 큰 꼭지점부터 트리에 추가하는 방식이 아니라, 임의의 시작점에서 출발하여 가중치가 가장 작은 변을 선택하면서 트리를 확장하는 방식이다. 즉, 현재 형성된 트리에서 인접한 최소 가중치의 변을 선택해 나가면서 최소 신장 트리를 구성한다. 선택지 1번은 신장 트리의 정의를 정확히 설명하고 있고, 선택지 2번도 최소 신장 트리의 정의를 올바르게 설명하고 있다. 선택지 3번의 크루스칼(Kruskal) 알고리즘 설명도 가중치가 작은 변을 선택하여 최소 신장 트리를 만드는 과정이 맞다.
돌발 1. 10개의 노드를 가지는 이진 트리의 최소 높이는 얼마인가?
1) 3
2) 4
3) 5
4) 6
정답: 1
해설: 이진 트리에서 높이 \( h \)일 때 최대 노드 수는 \( 2^{h+1} - 1 \)이다. 높이 3일 때 최대 노드 수는 \( 2^4 - 1 = 15 \)개이고, 높이 2일 때 최대 노드 수는 \( 2^3 - 1 = 7 \)개이다. 따라서 10개의 노드를 가지는 이진 트리의 최소 높이는 3이다. 선택지 2번은 15개의 노드까지 포함할 수 있어 불필요하게 높고, 선택지 3번과 4번은 더 높아 부적절하다.
12강. 조합이론
1. x+y+z = 5를 만족하는 자연수 x, y, z의 순서쌍 (x, y, z)의 개수를 구하면?
1) 5
2) 6
3) 8
4) 10
정답: 2
해설: \(x + y + z = 5\)를 만족하는 자연수 \(x, y, z\)의 순서쌍을 직접 계산해보면 다음과 같다. 가능한 값으로 \(x = 1, 2, 3\)일 때 각각의 경우를 고려한다. \(x = 1\)일 때, \(y + z = 4\)가 되어 가능한 쌍은 (1, 1, 3), (1, 2, 2), (1, 3, 1)이다. \(x = 2\)일 때, \(y + z = 3\)가 되어 가능한 쌍은 (2, 1, 2), (2, 2, 1)이다. \(x = 3\)일 때, \(y + z = 2\)가 되어 가능한 쌍은 (3, 1, 1)이다. 따라서 총 6개의 순서쌍이 있다.
2. 8비트 2진수 중 비트 111로 시작하거나 111로 끝나는 2진수의 개수는?
1) 16
2) 32
3) 60
4) 88
정답: 3
해설: 8비트 2진수 중 비트 111로 시작하는 경우와 111로 끝나는 경우를 고려하면 된다. 111로 시작하는 경우, 나머지 5비트는 자유롭게 변할 수 있어 \(2^5 = 32\)개가 있다. 111로 끝나는 경우도 나머지 5비트가 자유롭게 변할 수 있어 \(2^5 = 32\)개가 있다. 따라서, 두 조건을 모두 포함하면 \(32 + 32 = 64\)가 되는데, 시작과 끝이 동시에 111인 경우 \(2^2 = 4\)개를 중복 계산하므로 이를 빼야 한다. 최종적으로 \(64 - 4 = 60\)개가 된다. 선택지 1번과 2번은 조건을 충분히 고려하지 않았고, 선택지 4번은 중복을 제거하지 않아 부적절하다.
3. 1부터 5까지의 숫자를 가지고 만들 수 있는 3자리 수는 모두 몇 가지인가? (단, 각 숫자는 중복해서 사용하지 않는다고 가정함)
1) 8
2) 15
3) 27
4) 60
정답: 4
해설: 1부터 5까지의 숫자를 중복 없이 사용하여 3자리 수를 만드는 경우의 수는 순열을 이용해 계산할 수 있다. 첫 번째 자리에 5개의 숫자 중 하나를 선택하고, 두 번째 자리에 남은 4개 중 하나를 선택하며, 세 번째 자리에 남은 3개 중 하나를 선택하면 된다. 따라서 경우의 수는 \(5 \times 4 \times 3 = 60\)이다. 선택지 1번과 2번은 경우의 수를 충분히 고려하지 않았고, 선택지 3번은 계산이 잘못된 것이다. 따라서 정답은 4번 60이다.
4. 타일을 직렬로 6장을 붙이려고 한다. 준비된 타일은 금색이 1개, 은색이 3개, 검은색이 2개이다. 타일을 붙이는 방법은 모두 몇 가지인가?
1) 10
2) 30
3) 60
4) 64
정답: 3
해설: 8비트 2진수 중에서 비트 111로 시작하거나 111로 끝나는 경우를 고려하면, 먼저 각 경우의 수를 구해야 한다. 111로 시작하는 2진수는 나머지 5비트를 자유롭게 선택할 수 있어 $2^5 = 32$개이다. 111로 끝나는 2진수도 동일하게 $2^5 = 32$개이다. 하지만, 111로 시작하고 끝나는 경우는 중복되므로 이를 빼야 한다. 111로 시작하고 끝나는 2진수는 나머지 2비트를 자유롭게 선택할 수 있어 $2^2 = 4$개이다. 따라서, 총 개수는 $32 + 32 - 4 = 60$개이다.
5. 거실에 고흐 그림과 김환기 그림을 걸려고 한다. 그런데 그림을 걸 장소가 직렬로 모두 네 군데가 있다. 그림을 거는 방법은 모두 몇 가지인가?
1) 3
2) 6
3) 8
4) 12
정답: 4
해설: 네 군데 중 두 군데에 고흐와 김환기 그림을 각각 거는 경우의 수는 순서를 고려하여 계산하면 된다. 첫 번째 그림을 걸 수 있는 네 군데 중 한 군데를 선택하고, 두 번째 그림을 걸 수 있는 세 군데 중 한 군데를 선택하면 총 4 * 3 = 12가지 방법이 된다. 선택지 1번, 2번, 3번은 각각 3, 6, 8가지 방법으로 계산되며, 이 문제의 경우에는 적합하지 않다.
6. 1부터 5까지의 숫자를 가지고 만들 수 있는 3자리 수는 모두 몇 가지인가? (단, 각 숫자는 중복해서 사용할 수 있다고 가정함)
1) 27
2) 125
3) 128
4) 512
정답: 2
해설: 각 자리마다 1부터 5까지의 숫자를 사용할 수 있고 중복이 가능하므로, 각 자리는 5개의 선택지를 갖는다. 3자리 수를 만들기 위해 각 자리에 5개의 숫자가 가능하므로 전체 경우의 수는 $5 \times 5 \times 5 = 125$이다. 따라서 만들 수 있는 3자리 수의 총 개수는 125가지이다. 선택지 1번 27은 각 자리마다 3개의 숫자를 사용할 때의 경우의 수이고, 선택지 3번과 4번은 잘못된 계산으로 인해 부적절하다.
7. 8명으로 구성된 배구팀이 있다. 선발 출전할 선수로 6명을 뽑는 방법은 모두 몇 가지인가?
1) 28
2) 35
3) 49
4) 112
정답: 1
해설: 주어진 문제는 8명의 선수 중에서 6명을 선택하는 조합의 수를 구하는 것이다. 조합의 수는 $\binom{n}{k}$로 계산하며, 이는 $\frac{n!}{k!(n-k)!}$의 식을 따른다. 여기서 $n$은 총 선수의 수 8명, $k$는 선발할 선수의 수 6명이다. 따라서 $\binom{8}{6} = \frac{8!}{6!(8-6)!} = \frac{8!}{6!2!}$이다. 이를 계산하면 $\frac{8 \times 7}{2 \times 1} = 28$이므로 정답은 1번이다.
8. (𝑥+𝑦)⁶ 에서 𝑥⁴ 𝑦² 의 계수는?
1) 6
2) 12
3) 15
4) 30
정답: 3
해설: 이 문제는 이항 정리를 사용하여 해결할 수 있다. 이항 정리에 따르면 \((x + y)^n\)의 전개에서 \(x^a y^b\) 항의 계수는 \(\binom{n}{a}\)이다. 여기서 \(\binom{n}{a}\)는 이항 계수로, \(\frac{n!}{a!(n-a)!}\)로 계산된다. 문제에서 \(n = 6\), \(a = 4\), \(b = 2\)이므로 계수는 \(\binom{6}{4} = \frac{6!}{4!2!} = \frac{720}{24 \times 2} = 15\)이다. 따라서 \(x^4 y^2\)의 계수는 15이다.
9. 자루에 감자 7개와 고구마 13개가 들어 있는데, 감자는 6개가 상했고 고구마는 2개가 상했다고 가정하자. 만일 자루에서 상한 것을 하나 꺼냈는데 그것이 고구마일 확률을 구하면? (지문의 힌트 참고)

1) 1/10
2) 1/4
3) 13/20
4) 2/5
정답: 2
해설: 상한 것을 꺼낼 때 그것이 고구마일 확률 P(A|B)는 조건부 확률로 구할 수 있다. 상한 것을 꺼내는 사건을 B, 상한 고구마를 꺼내는 사건을 A라고 하면, P(A∩B)는 상한 고구마의 개수 2개를 전체 구슬 개수 20개로 나눈 값인 2/20이다. P(B)는 상한 감자와 고구마를 꺼낼 확률로, (6+2)/20 = 8/20이다. 따라서 P(A|B) = (2/20) / (8/20) = 2/8 = 1/4이다. 다른 선택지는 조건부 확률을 잘못 계산한 경우이다.
10. 다음 지문에 보이는 점화식의 해를 구하면?

1) ① 번
2) ② 번
3) ③ 번
4) ④ 번
정답: 4
해설: 주어진 점화식을 푸는 방법은 먼저 점화식의 형태를 확인하는 것이다. 점화식이 \(a_{n+1} = r \cdot a_n + d\) 형태라면 이는 1차 선형 점화식이다. 이러한 점화식의 일반해는 \(a_n = A \cdot r^n + B\) 형태로 나타낼 수 있다. 이를 이용하여 초기 조건을 적용하고 상수 \(A\)와 \(B\)를 구하면 된다. 선택지 4번이 이러한 점화식의 해와 일치한다.
13강. 정수론
1. a, b, c가 정수이고, a|b, a|c (단, c≠0)일 때, 다음 중 옳지 않은 것은?
1) a|(b+c)
2) a|(b-c)
3) a|(b×c)
4) a|(b÷c)
정답: 4
해설: a가 b와 c의 약수일 때, a는 b+c, b-c, b×c 모두 나눌 수 있다. 이는 a|b와 a|c가 성립하면, a|(b+c)와 a|(b-c), a|(b×c)가 성립함을 의미한다. 하지만 a|c가 성립해도, b가 a로 나누어떨어진다고 해서 b를 c로 나눈 값이 a로 나누어떨어진다는 보장은 없다. 따라서 a|(b÷c)는 항상 성립하지 않는다. 선택지 1, 2, 3은 모두 옳다.
2. 유클리드 호제법을 이용하여 gcd(210, 770)을 구하면?
1) 15
2) 30
3) 70
4) 105
정답: 3
해설: 유클리드 호제법은 두 수의 최대공약수를 구하는 알고리즘이다. 770을 210으로 나눈 나머지는 140, 210을 140으로 나눈 나머지는 70, 140을 70으로 나눈 나머지는 0이다. 나머지가 0이 될 때의 나누는 수가 최대공약수이다. 따라서 gcd(210, 770)은 70이다. 선택지 1번, 2번, 4번은 모두 최대공약수가 아니다.
3. 30m × 36m 크기의 직사각형 바닥에 빈자리가 없도록 타일을 깔고자 하는데, 동일한 크기의 정사각형 타일만 사용한다고 하면, 필요한 타일의 최소 개수는?
1) 30
2) 36
3) 40
4) 90
정답: 1
해설: 직사각형 바닥에 빈자리가 없도록 동일한 크기의 정사각형 타일을 사용하려면, 30m와 36m의 최대공약수를 구해야 한다. 30과 36의 최대공약수는 6이므로, 한 변의 길이가 6m인 정사각형 타일을 사용하면 된다. 30m × 36m 크기의 바닥을 6m × 6m 타일로 덮으면, 가로에는 5개, 세로에는 6개의 타일이 필요하다. 따라서 총 필요한 타일의 개수는 5 × 6 = 30개이다. 다른 선택지는 타일의 크기를 고려하지 않고 계산한 잘못된 값이다.
4. 다음 중 옳지 않은 것은?
1) 14 ≡ 36 ( mod 11)
2) 10 ≡ 40 ( mod 11)
3) 24 ≡ 46 ( mod 11)
4) 29 ≡ 18 ( mod 11)
정답: 2
해설: 모듈러 연산에서 두 수가 동치가 되려면, 두 수를 나눈 나머지가 같아야 한다. 1번은 14와 36을 11로 나눈 나머지가 각각 3으로 동일하다. 2번은 10과 40을 11로 나눈 나머지가 각각 10과 7로 다르다. 3번은 24와 46을 11로 나눈 나머지가 각각 2로 동일하다. 4번은 29와 18을 11로 나눈 나머지가 각각 7로 동일하다. 따라서 2번이 옳지 않은 것이다.
5. a, b가 정수이고 𝒂 ≡ 𝒃 ( mod 5 )일 때 다음 중 옳지 않은 것은?
1) 5 | ( a + b )
2) 5 | ( a - b )
3) 𝒂 mod 5 = 𝒃 mod 5
4) 𝒂 = 5𝒌 + 𝒃 (단, 𝒌는 정수)
정답: 1
해설: a ≡ b (mod 5)일 때, a와 b의 차는 5의 배수이므로 5 | (a - b)이다. 따라서 2번은 맞는 표현이다. 또한, a와 b를 5로 나눈 나머지는 같으므로 3번도 맞다. 4번은 a가 b에 5의 배수를 더한 형태로 표현될 수 있어 맞다. 하지만 5 | (a + b)는 두 수의 합이 5의 배수라는 의미로 이는 항상 성립하지 않으므로 옳지 않다.
6. a, b, c가 정수이고 𝒂 ≡ 𝒃 (mod 𝒎 )일 때 다음 중 옳지 않은 것은?
1) 𝒂 + 𝒄 ≡ 𝒃 + 𝒄 ( mod 𝒎 )
2) 𝒂 𝒄 ≡ 𝒃 𝒄 ( mod 𝒎 )
3) 𝒂 ≡ 𝒂 𝒃 ( mod 𝒎 )
4) 𝒂 ≡ 𝒂 + 𝒃 𝒎 ( mod 𝒎 )
정답: 3
해설: 모듈로 연산에서 a ≡ b (mod m)이면, a와 b는 m으로 나눴을 때 같은 나머지를 갖는다. 예를 들어, a ≡ 2, b ≡ 5 (mod 3)일 때 1번은 양변에 c를 더해도 동일한 나머지를 가지므로 옳다. 즉, 2 + c ≡ 5 + c (mod 3)은 항상 성립한다. 2번은 양변에 c를 곱해도 동일한 나머지를 가지므로 옳다. 예를 들어, 2 * c ≡ 5 * c (mod 3)은 항상 성립한다. 4번은 a와 (a + b * m)은 b * m이 m으로 나누어 떨어지므로 나머지가 같아 옳다. 예를 들어, 2 ≡ 2 + 5 * 3 (mod 3)은 성립한다. 3번은 a와 a * b는 일반적으로 같은 나머지를 가지지 않으므로 옳지 않다. 예를 들어, 2 ≡ 2 * 5 (mod 3)은 성립하지 않는다.
7. 다음 빈 칸에 적당한 말들을 순서대로 적은 것은?
𝒏이 2 이상의 자연수이면 𝒏은 ( )이거나 소수의 ( )으로 유일하게 표현할 수 있다.
1) 합성수, 합
2) 합성수, 곱
3) 소수, 합
4) 소수, 곱
정답: 4
해설: 모든 자연수 \( n \geq 2 \)는 소수이거나 소수의 곱으로 유일하게 표현할 수 있다. 이는 소수의 곱셈이 이루어지는 유일한 방식인 소인수 분해에 기반한 것으로, 소인수 분해 정리에 따르면 각 자연수는 소수들의 곱으로만 구성된다. 선택지 1과 2에서 '합성수'는 자연수의 성질을 완전히 설명하지 않으며, '합'이라는 표현은 적절하지 않다. 선택지 3에서는 '소수의 합'으로 유일하게 표현할 수 없으므로 틀리다. 따라서 정답은 4번 '소수, 곱'이다.
8. 다음 중 메르센 소수가 아닌 것은?
1) 3
2) 7
3) 11
4) 15
정답: 3
해설: 메르센 소수는 \(2^p - 1\) 형태로 나타나는 소수이다. \(3\)은 \(2^2 - 1\), \(7\)은 \(2^3 - 1\), \(11\)은 \(2^5 - 1\)이 아니며, \(15\)는 \(2^4 - 1\)로 소수가 아니다. 따라서 \(11\)은 메르센 소수이다. 선택지 \(1\), \(2\), \(4\)는 메르센 수이거나 소수가 아닌 형태를 가지고 있다.
9. 페르마의 작은 정리를 이용하여 2¹⁰⁰을 5로 나누었을 때의 나머지를 구하면 (Hint: 2⁵⁻¹ = 2⁴ ≡ 1 ( mod 5 ) )?
1) 1
2) 2
3) 3
4) 4
정답: 1
해설: 페르마의 작은 정리에 따르면, 소수 \( p \)와 정수 \( a \)가 서로 소일 때 \( a^{p-1} \equiv 1 \pmod{p} \)이다. 여기서 \( a = 2 \)이고 \( p = 5 \)이므로 \( 2^4 \equiv 1 \pmod{5} \)이다. 따라서 \( 2^{100} = (2^4)^{25} \equiv 1^{25} \equiv 1 \pmod{5} \)가 되어 나머지는 1이다. 선택지 2, 3, 4는 모두 페르마의 작은 정리에 의해 틀리다.
10. 나머지 거듭제곱 알고리즘을 활용하여 3⁵ mod 7을 구하면?
1) 6
2) 5
3) 4
4) 3
정답: 2
해설: 나머지 거듭제곱 알고리즘을 사용하여 $3^5 \mod 7$을 구하면, $3^2 = 9 \equiv 2 \mod 7$이고, 이를 다시 제곱하여 $3^4 \equiv 2^2 = 4 \mod 7$이다. 마지막으로 $3^5 \equiv 3^4 \cdot 3 \equiv 4 \cdot 3 = 12 \equiv 5 \mod 7$이다. 따라서 정답은 2번 5이다. 다른 선택지 1, 3, 4는 올바른 계산 결과가 아니다.
돌발 1. m 이 1 보다 큰 정수이고, a, b, c 를 임의의 정수이며, a ≡ b ( mod m )이고, c ≡ d ( mod m )이라고 할 때, 다음 중 부적절한 것은?
1) b ≡ a ( mod m )
2) ac ≡ bd ( mod m )
3) a + b ≡ c + d ( mod m )
4) a + c ≡ b + d ( mod m )
정답: 3
해설: 모듈로 연산에서 \(a \equiv b \ (\text{mod} \ m)\)과 \(c \equiv d \ (\text{mod} \ m)\)이면, \(b \equiv a \ (\text{mod} \ m)\)은 성립하고, \(ac \equiv bd \ (\text{mod} \ m)\)도 성립한다. 또한, \(a + c \equiv b + d \ (\text{mod} \ m)\)도 성립한다. 하지만 \(a + b \equiv c + d \ (\text{mod} \ m)\)은 두 독립적인 합이므로 성립하지 않는다. 따라서 선택지 3번이 부적절하다.
돌발 2. 다음 중 내용이 올바른 것은?
1) 소수는 유한하다.
2) 1보다 크면서 소수가 아닌 자연수는 소인수라고 부른다.
3) n 이 합성수라면 n 의 소인수 중 하나는 1n n 보다 작거나 같다.
4) 1 보다 큰 자연수 n 의 약수가 1 과 n 뿐일 때, n 을 소수라고 한다.
정답: 4
해설: 1보다 큰 자연수 \( n \)의 약수가 1과 \( n \)뿐일 때, \( n \)은 소수이다. 선택지 1번은 소수는 무한히 많으므로 틀리다. 선택지 2번에서 소수가 아닌 자연수는 합성수라고 부른다. 선택지 3번의 내용에서 합성수 \( n \)의 소인수 중 하나는 \(\sqrt{n}\) 이하이어야 한다. 따라서 선택지 4번이 올바른 내용이다.
14강. 오토마타 및 형식 언어
1. 튜링머신에 대한 서술로서 옳지 않은 것은?
1) 테이프는 셀로 구분되어 있다.
2) 헤드는 테이프 위의 심벌을 읽거나 쓸 수 있다.
3) 상태 기록부에서 기록할 수 있는 상태의 개수는 무한하다.
4) 유한한 표에는 수행해야 할 작업들이 기술되어 있다.
정답: 3
해설: 튜링머신의 상태 기록부에서 기록할 수 있는 상태의 개수는 유한하다. 선택지 1번은 테이프가 셀로 구분된다는 점에서 맞는 설명이다. 선택지 2번은 헤드가 테이프 위의 심벌을 읽거나 쓸 수 있다는 점에서 정확하다. 선택지 4번은 유한한 표에 수행해야 할 작업들이 기술된다는 점에서 올바르다. 반면 선택지 3번은 잘못된 설명으로, 상태의 개수는 유한하다.
2. 형식 문법의 포함 관계로 옳은 것은?
1) 정규 문법 ⊂ 문맥 자유 문법 ⊂ 무제약 문법 ⊂ 문맥 의존 문법
2) 정규 문법 ⊂ 문맥 자유 문법 ⊂ 문맥 의존 문법 ⊂ 무제약 문법
3) 문맥 자유 문법 ⊂ 정규 문법 ⊂ 무제약 문법 ⊂ 문맥 의존 문법
4) 정규 문법 ⊂ 무제약 문법 ⊂ 문맥 자유 문법 ⊂ 문맥 의존 문법
정답: 2
해설: 형식 언어의 포함 관계는 정규 문법 ⊂ 문맥 자유 문법 ⊂ 문맥 의존 문법 ⊂ 무제약 문법 순서이다. 정규 문법은 가장 제한적이며, 문맥 자유 문법은 이를 포함한다. 문맥 의존 문법은 문맥 자유 문법을 포함하고, 무제약 문법은 모든 문법을 포함한다. 선택지 1은 문맥 의존 문법과 무제약 문법의 순서가 잘못되었고, 선택지 3과 4는 각 문법의 포함 관계가 틀렸다.
3. 유한 오토마타를 구성하는 것으로 부적절한 것은?
1) 상태전이도
2) 상태전이 함수
3) 입력기호의 유한집합
4) 상태의 유한집합
정답: 1
해설: 유한 오토마타는 다섯 가지 구성 요소를 포함한다. 상태의 유한집합, 입력기호의 유한집합, 시작 상태, 상태전이 함수, 그리고 하나 이상의 최종 상태이다. 상태전이 함수는 오토마타의 상태와 입력기호에 따라 다음 상태를 결정한다. 상태전이도는 오토마타의 동작을 시각적으로 나타낸 도구일 뿐, 오토마타의 구성 요소는 아니다. 선택지 2, 3, 4는 모두 유한 오토마타의 구성 요소에 해당한다.
4. 다음 상태전이도는 어떤 유한 오토마타 𝑴을 표현하고 있는데, 𝑴에 대해 입력 문자열 0011에 대응하는 출력 문자열로서 옳은 것은?

1) 𝒂𝒃𝒂𝒃
2) 𝒂𝒃𝒃𝒂
3) 𝒂𝒂𝒃𝒃
4) 𝒃𝒂𝒃𝒂
정답: 2
해설: 입력 문자열 0011을 따라가며 각 상태에서 대응하는 출력을 추적해야 한다. 시작 상태 \( s_0 \)에서 입력 0은 \( s_1 \)로 이동하며 출력은 \( a \)이다. \( s_1 \)에서 입력 0은 \( s_1 \)에 머물며 출력은 \( b \)이다. 다음 입력 1은 \( s_0 \)로 이동하며 출력은 \( b \)이다. 마지막 입력 1은 \( s_0 \)에 머물며 출력은 \( a \)이다. 따라서 최종 출력 문자열은 \( abba \)이다. 선택지 1, 3, 4는 잘못된 출력을 나타낸다.
5. 다음 상태전이도는 어떤 결정적 유한 오토마타 𝑴을 표현하고 있는데, 𝑴이 수락하는 문자열은?

1) 0 0 1 1
2) 0 1 0 1
3) 0 0 0 1
4) 0 1 0 0
정답: 4
해설: 상태전이도를 따라가며 각 입력 문자열이 최종 상태로 이동하는지 확인한다. \( s_0 \)에서 시작하여 입력 0을 받으면 \( s_1 \)로 이동하고, \( s_1 \)에서 입력 1을 받으면 \( s_2 \)로 이동하며, \( s_2 \)에서 입력 0을 받으면 \( s_2 \)에 머문다. 따라서 "0 1 0 0" 입력 시 최종 상태 \( s_2 \)에 도달한다. 선택지 1, 2, 3은 최종 상태에 도달하지 않으므로 수락되지 않는다.
※ (6~7) 다음 상태전이도는 어떤 마르코프 연쇄를 표현한 것이다. 물음에 답하시오.
6. 지문에서 해당 마르코프 연쇄를 전이확률행렬로 표시한 것으로 옳은 것은?

1)

2)

3)

4)

정답: 4
7. 지문에서, 상태 0은 “맑음”을, 상태 1은 “비가 옴”을 나타낸다고 할 때, 오늘의 날씨 상태가 “맑음”일 때 내일의 날씨가 “비가 옴”이 될 확률은?
1) 30%
2) 40%
3) 50%
4) 60%
정답: 2
해설: 상태 0은 "맑음", 상태 1은 "비가 옴"을 나타낸다. 현재 상태가 0일 때 다음 상태가 1로 전이될 확률을 구한다. 상태 0에서 상태 1로 전이될 확률은 0.4이다. 따라서 오늘 날씨가 맑음일 때 내일 날씨가 비가 올 확률은 40%이다. 선택지 1, 3, 4는 각각 30%, 50%, 60%의 확률을 나타내지만, 이는 주어진 상태전이도에서 맑음에서 비가 옴으로 전이되는 확률과 일치하지 않는다.
8. 언어 𝑳 = { 𝒂, 𝒃 }일 때 𝑳³ 의 원소로서 옳은 것은?
1) 𝒂𝒃𝒂
2) 𝒂𝒃
3) 𝒂
4) ⋋
정답: 1
해설: 언어 L의 원소는 {a, b}이고, L³은 L의 원소를 세 번 이어 붙인 문자열의 집합이다. 즉, L³의 원소는 길이가 3인 모든 문자열로 이루어진다. 따라서 a, b로 구성된 길이가 3인 문자열은 aba, aaa, bbb, aab 등이다. 선택지 1) aba는 이 조건에 맞는 반면, 선택지 2) ab는 길이가 2로 짧고, 선택지 3) a는 길이가 1로 짧으며, 선택지 4) ⋋는 공백 문자열로 길이가 0이므로 L³의 원소가 아니다.
9. 알파벳 Σ = { 𝒂, 𝒃, 𝒄 }를 통해서 만들어 낼 수 있는 문자열이 아닌 것은?
1) 𝒄𝒃𝒂
2) 𝒃𝒃𝒃
3) 010
4) ⋋
정답: 3
해설: 알파벳 Σ = {𝒂, 𝒃, 𝒄}를 통해 만들어 낼 수 있는 문자열은 이 집합에 속하는 문자들로만 이루어져야 한다. 선택지 1) 𝒄𝒃𝒂와 선택지 2) 𝒃𝒃𝒃는 모두 Σ의 문자로 구성된 문자열이다. 선택지 4) ⋋는 집합에 속하지 않는 문자이지만 특수 기호로 간주될 수 있다. 선택지 3) 010은 숫자 0과 1로 이루어져 있어 Σ에 포함되지 않으므로 정답이다.
10. 문법 G = ( {S }, { 𝒂, 𝒃 }, { S → 𝒂S𝒃, S → λ }, S ) 의 문법 언어 𝑳 (G ) 는 무엇인가?
1) 𝑳 (G ) = { 𝒂, 𝒂𝒂, 𝒂𝒂𝒂, ... }
2) 𝑳 (G ) = { 𝒃, 𝒃𝒃, 𝒃𝒃𝒃, ... }
3) 𝑳 (G ) = { 𝒂𝒃, 𝒂𝒂𝒃𝒃, 𝒂𝒂𝒂𝒃𝒃𝒃, ... }
4) 𝑳 (G ) = { 𝒂𝒃, 𝒂𝒃𝒂𝒃, 𝒂𝒃𝒂𝒃𝒂𝒃, ... }
정답: 3
해설: 주어진 문법은 $S \to aSb$와 $S \to \lambda$로 정의되며, 이는 $S$가 빈 문자열이 되거나 $a$와 $b$가 쌍으로 반복되는 패턴을 생성함을 의미한다. 따라서 언어 $L(G)$는 $a$와 $b$가 동일한 수로 배치된 문자열들로 구성된다. 1번과 2번은 각각 $a$와 $b$만 포함된 문자열이라 부적절하고, 4번은 $a$와 $b$가 교대로 나오는 형태라 부적절하다. 3번이 정답으로, $L(G) = \{ab, aabb, aaabbb, \ldots\}$이다.
돌발 1. 대표적인 오토마타인 튜링 머신의 구성 요소가 아닌 것은?
1) 무한의 길이를 갖는 테이프(tape)
2) 테이프 위에서 기호를 읽거나 쓸 수 있는 헤더(header)
3) 튜링 머신의 입력을 기록하는 입력 기록부(input register)
4) 튜링 머신이 어떤 상태에서 수행해야 할 작업이 서술되어 있는 휴한한 표(finite table)
정답: 3
해설: 튜링 머신의 구성 요소에는 무한 길이의 테이프(tape), 테이프 위에서 기호를 읽거나 쓰는 헤더(header), 그리고 상태와 수행 작업이 서술된 유한한 표(finite table)가 있다. 하지만 입력을 기록하는 입력 기록부(input register)는 튜링 머신의 구성 요소가 아니다. 선택지 1번, 2번, 4번은 모두 튜링 머신의 필수적인 구성 요소이다.
15강. 종합 정리
1. 다음 중 이산수학에서 다루는 대상이 아닌 것은?
1) 명제
2) 정수
3) 그래프
4) 미적분
정답: 4
해설: 이산수학은 명제, 정수, 그래프와 같은 이산적 구조를 연구하는 학문이다. 명제는 논리학에서, 정수는 수론에서, 그래프는 그래프 이론에서 다루는 중요한 주제이다. 반면, 미적분은 연속적인 변화를 다루는 미분과 적분을 포함하는 학문으로, 주로 해석학에서 다루어진다. 따라서 미적분은 이산수학의 대상이 아니다.
2. 행렬에 대한 다음 서술 중 옳은 것은?
1) 행렬끼리의 곱연산은 교환법칙이 성립한다.
2) 정방행렬은 행의 수와 열의 수가 같은 행렬이다.
3) 정방행렬이라면 언제나 자신의 역행렬을 갖는다.
4) 대각원소가 모두 1인 행렬을 단위행렬이라고 한다.
정답: 2
해설: 정방행렬은 행과 열의 수가 같은 행렬을 말한다. 1번은 행렬의 곱셈은 교환법칙이 성립하지 않기 때문에 틀리다. 3번은 정방행렬이라고 해서 반드시 역행렬이 존재하는 것은 아니며, 역행렬이 존재하려면 행렬식이 0이 아니어야 한다. 4번은 대각원소가 모두 1인 행렬은 단위행렬이라 할 수 있지만, 단위행렬은 추가로 나머지 원소가 모두 0이어야 한다.
3. 다음 중 관계를 표현하는 방법으로 부적절한 것은?
1) 화살표 도표
2) 방향 그래프
3) 순서도
4) 부울행렬
정답: 3
해설: 관계를 표현하는 방법으로 화살표 도표, 방향 그래프, 부울행렬은 적절하다. 화살표 도표는 관계를 시각적으로 보여주고, 방향 그래프는 노드 간의 방향성 있는 연결을 나타내며, 부울행렬은 관계를 행렬 형태로 표현한다. 그러나 순서도는 알고리즘이나 프로세스를 단계별로 표현하는 도구로, 관계를 표현하는 데 부적절하다. 선택지 1, 2, 4는 관계를 명확히 나타낼 수 있다.
4. 다음 지문의 내용 중 옳은 것은?

1) ①
2) ②
3) ③
4) ④
정답: 4
해설: 첫 번째 식 ①은 $\left\lfloor 12.34 \right\rfloor = 12$로, 내림 연산이므로 옳다. 두 번째 식 ②는 $\left\lfloor -0.917 \right\rfloor = -1$로, 절댓값 연산을 잘못 적용하였다. 세 번째 식 ③은 $5! = 120$이므로 틀렸다. 네 번째 식 ④는 $27 \mod 5 = 2$로, 나머지 연산이 옳다. 따라서 4번이 정답이다.
5. 다음 괄호 안에 들어갈 용어들을 순서대로 나열한 것은?

1) 변, 동형, 사이클, 단순
2) 변, 인접, 루프, 병렬
3) 꼭짓점, 인접, 루프, 단순
4) 그래프, 동형, 루프, 병렬
정답: 2
해설: 그래프 \( G \)는 꼭짓점의 집합 \( V \)와 변의 집합 \( E \)를 가지며, 변은 두 꼭짓점을 연결하는 역할을 수행한다. 연결된 두 꼭짓점은 서로 인접한다고 한다. 동일한 꼭짓점을 연결하는 변은 특별히 루프라 하고, 동일한 두 꼭짓점을 연결하는 여러 개의 변은 병렬 변이라 한다. 선택지 2번이 모든 괄호에 알맞은 용어를 순서대로 포함하고 있다.
6. 다음 그래프 중에서 트리가 아닌 것은?
1)

2)

3)
4)

정답: 3
7. 다음 괄호 안에 들어갈 용어들을 순서대로 나열한 것은?

1)

2)

3)

4)

정답: 4
8. 다음 괄호 안에 들어갈 용어로서 옳은 것은?

1) 최대공약수
2) 최소공배수
3) 합성수
4) 소수
정답: 1
'방통대' 카테고리의 다른 글
| 방송대 모바일프로그래밍 2012학년도 2학기 기말시험 기출문제 풀이 및 다운로드 (0) | 2024.06.01 |
|---|---|
| 방통대 모바일앱프로그래밍 2011학년도 2학기 기말고사 기출문제 풀이 및 정답 다운로드 (1) | 2024.06.01 |
| 방통대 인공지능 2017-2 기출문제 및 풀이 다운로드 (0) | 2024.05.21 |
| 방통대 인공지능 2016-2 기말시험 기출문제 문제 풀이 및 다운로드 (1) | 2024.05.20 |
| 방통대 파이썬 프로그래밍 기말시험 대비 심화 연습문제 풀이 및 해설 (0) | 2024.05.20 |


